如图所示，空间分布着方向平行于纸面且与场区边界垂直的有界匀强电场，电场强度为E、宽度为L。在紧靠电场右侧的圆形区域内，分布着垂直于纸面向外的匀强磁场，圆形磁场区域半径为r。当一带正电的粒子（质量为m，电荷量为q）从A点静止释放后，在M点离开电场，并沿半径方向射入磁场区域，磁感应强度为B，粒子恰好从N点射出，O为圆心，∠MON＝120°，粒子重力忽略不计。求：
（1）粒子经电场加速后，进入磁场时速度v的大小；
（2）匀强磁场的磁感应强度B的大小和粒子在电场、磁场中运动的总时间t；
（3）若粒子在离开磁场前某时刻，磁感应强度方向不变，大小突然变为B1，此后粒子恰好被束缚在该磁场中，则B1的最小值为多少？
昆明市西山区团结乡建有滑草场。可将其看成倾角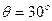
的斜面，一游客连同滑草装备的总质量为
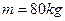，他从静止开始匀加速下滑，在
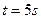时间内沿直线滑下
（不计空气阻力，取g=10m/s2，结果保留2位有效数字）
（1）游客连同装备下滑过程中受到的摩擦力F为多大？
（2）滑草装置与草地之间的动摩擦因数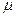
为多大？
如
图所示，质量为m1的物体甲通过三段轻绳悬挂，三段轻绳的结点为O。轻绳OB水平且B端与放置在水平面上的质量为m2的物体乙相连，轻绳OA与竖直方向的夹角θ＝37°，物体甲、乙均处于静止状态。（取g=10m/s2，sin37°=0.6，cos37°=0.8，设最大静摩擦力等于滑动摩擦力）求：
（1）轻绳OA、OB受到的拉力是多大。
（2）若物体乙的质量m2=4kg，物体乙与水平面之间的动摩擦因数为μ=0.3，则欲使物体乙在水平面上不滑动，物体甲的质量m1最大不能超过多少？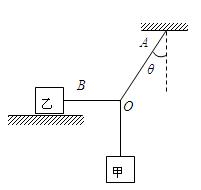 
两个完全相同的物体A、B，在同一粗糙水平面上以相同的初速度从同一位置开始运动。图中的两条直线分别表示A物体受到水平拉力F=0.8N作用和B物体不受拉力作用的v-t图像，求：
（1）A、B运动的加速度；
（2）12s末A、B间的距离；
（3）两物体的量质。
如图所示，传送带与地面的倾角为37°，以10m/s的速率逆时针转动，在传送带上方轻
轻静放一质量为0.5kg的物块，它与传送带间的动摩擦因数为0.5，传送带两轮间距为16m，则物块从上端运动到下端所需时间为多少？(g取10m/s2，sin370=0.6，cos370=0.8)
物体B放在物体A上，A、B的上下表面均与斜面平行（如图），A、B的质量分别为M、m，A与斜面的动摩擦因数为ц1，B与A的动摩擦因数为ц2，当两者从静止开始以相同的加速度从固定斜面滑下时，滑块B受到的摩擦力是多少？