某小学为每个班级配备了一种可
以加热的饮水机，该饮水机的工作程序是：放满水后，
接通电源，则自动开始加热，每分钟水温上升10ºC，待加热到100ºC，饮水机自动切断电源，水温开始下降，水温和时间成反比例关系，直至水温降至室温，饮水机再次自动加热，重复上述过程．设某天水温和室温为20ºC，接通电源后，水温和时间的关系下图所示，回答下列问题；
（1）分别求出0≤x≤8和8＜x≤a时，y和x之间的关系式；
（2）求出图中a的值．
（3）下表是该小学的作息时间，若同学们希望在上午第一节下课8：20时能喝到不超过
40ºC的开水，已知第一节下课前无人接水，请直接写出生活委员应该在什么时间或时间段接通饮水机电源（不可以用上课时间）．
 |
| 时间 |
节次 |
|
| 上午 |
7：20 |
到校 |
| 7：45~8：20 |
第一节 |
|
| 8：30~9：05 |
第二节 |
|
| …… |
…… |
如图，在等腰梯形ABCD中，AD∥BC，AB＝DC＝5，AD＝6，BC＝12.动点P从D点出发沿DC以每秒1个单位的速度向终点C运动，动点Q从C点出发沿CB以每秒2个单位的速度向B点运动．两点同时出发，当P点到达C点时，Q点随之停止运动．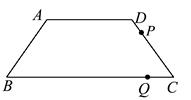
(1)梯形ABCD的面积等于________；
(2)当PQ∥AB时，P点离开D点的时间等于______秒；
(3)当P、Q、C三点构成直角三角形时，P点离开D点多长时间？
已知：如图，在正方形
中，点
、
分别在
和
上，
．
（1）求证：
；
（2）连接
交
于点
，延长
至点
，使
，连接
、
，判断四边形
是什么特殊四边形？并证明你的结论．
如图所示，在△ABC中，D是AC的中点，E是线段BC延长线上一点，过点A作BE的平行线与线段ED的延长线交于点F，连结AE、CF.
(1)求证：AF＝CE；
(2)若AC＝EF，试判断四边形AFCE是什么样的四边形，并证明你的结论
如图，在△ABC中，点O是AC边上的一个动点，过点O作直线MN∥BC，设MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F.
(1)求证：EO＝FO；
(2)当点O运动到何处时，四边形AECF是矩形？并证明你的结论．
(3)在(2)的条件下，当△ABC满足什么条件时，四边形AECF是正方形？
如图，正方形ABCD绕点A逆时针旋转no后得到正方形AEFG，EF与CD交于点O．
（1）以图中已标有字母的点为端点连结两条线段（正方形的对角线除外），要求所连结的两条线段相交且互相垂直，并说明这两条线段互相垂直的理由；
（2）若正方形的边长为2cm，重叠部分（四边形AEOD）的面积为
cm2，求旋转的角度n．