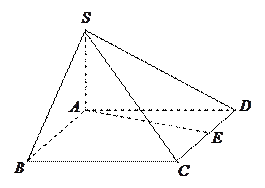本题有(1)、(2)、(3)三个选答题,每小题7分,请考生任选2题作答,满分14分,如果多做,则按所做的前两题计分.作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中.
(1)(本小题满分7分)选修4-2:矩阵与变换
已知矩阵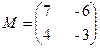 ,向量
,向量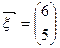 .
.
(I)求矩阵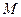 的特征值
的特征值 、
、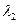 和特征向量
和特征向量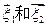 ;
;
(II)求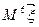 的值.
的值.
(2)(本小题满分7分)选修4-4:坐标系与参数方程
在平面直角坐标系xOy中,已知曲线C的参数方程为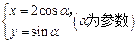 .以直角坐标系原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
.以直角坐标系原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为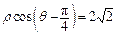 .
.
(Ⅰ)求直线l的直角坐标方程;
(Ⅱ)点P为曲线C上的动点,求点P到直线l距离的最大值.
(3)(本小题满分7分)选修4-5:不等式选讲
(Ⅰ)已知:a、b、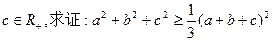 ;
;
(Ⅱ)某长方体从一个顶点出发的三条棱长之和等于3,求其对角线长的最小值.
(本小题满分12分)
某货轮在A处看灯塔B在货轮北偏东 ,距离为
,距离为 n mile;在A处看灯塔C在货轮的北偏西
n mile;在A处看灯塔C在货轮的北偏西 ,距离为
,距离为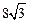 n mile.货轮由A处向正北航行到D处时,再看灯塔B在北偏东
n mile.货轮由A处向正北航行到D处时,再看灯塔B在北偏东 ,求:
,求:
(Ⅰ)A处与D处之间的距离;
(Ⅱ)灯塔C与D处之间的距离.
(本小题 满分12分)
满分12分)
已知等差数列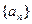 满足
满足
(1)求数列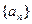 的通项公式;
的通项公式;
(2)设各项均为正数的等比数列 的前n项和为Tn若
的前n项和为Tn若 求
求
(本小题满分14分)
设数列 的通项公式为
的通项公式为 . 数列
. 数列 定义如下:对于正整数m,
定义如下:对于正整数m,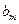 是使得不等式
是使得不等式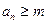 成立的所有n中的最小值.
成立的所有n中的最小值.
(Ⅰ)若 ,求
,求 ;
;
(Ⅱ)若 ,求数列
,求数列 的前2m项和公式;
的前2m项和公式;
(Ⅲ)是否存在p和q,使得 ?如果存在,求p和q的取值范围;如果不存在,请说明理由.
?如果存在,求p和q的取值范围;如果不存在,请说明理由.
(本小题满分14分)
已知圆 方程为:
方程为: .
.
(Ⅰ)直线 过点
过点 ,且与圆
,且与圆 交于
交于 、
、 两点,若
两点,若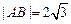 ,求直线
,求直线 的方程;
的方程;
(Ⅱ)过圆 上一动点
上一动点 作平行于
作平行于 轴的直线
轴的直线 ,设
,设 与
与 轴的交点为
轴的交点为 ,若向量
,若向量 ,求动点
,求动点 的轨迹方程,并说明此轨迹是什么曲线.
的轨迹方程,并说明此轨迹是什么曲线.
(本小题满分14分)
如图,在四棱锥 中,
中, ,
,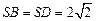 ,底面
,底面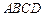 是菱形,且
是菱形,且 ,
,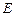 为
为 的中点.
的中点.
(Ⅰ)证明: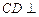 平面
平面 ;
;
(Ⅱ)侧棱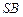 上是否存在点
上是否存在点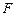 ,使得
,使得 平面
平面 ?并证明你的结论.
?并证明你的结论.