已知某运动员每次投篮命中的概率都为40%。现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率：先由计算器算出0到9之间取整数值的随机数，指定1，2，3，4表示命中，5，6，，7，8，9，0表示不命中；再以每三个随机数为一组，代表三次投篮的结果。经随机模拟产生了20组随机数： 907 966 191 925 271 932 812 458 569 683 431 257 393 027 556 488 730 113 537 989
据此估计，该运动员三次投篮恰有两次命中的概率为
A．0.35 B 0.25 C 0.20 D 0.15
已知集合
( )
A． |
B． |
C． |
D． |
给出下列结论：①若
，
，则
； ②若
，则
；
③
； ④
；⑤若
其中正确的为（）
| A．②③④ | B．①②⑤ | C．④⑤ | D．③④⑤ |
函数
是（）
A．最小正周期为 的奇函数 |
B．最小正周期为 的奇函数 |
| C．最小正周期为的偶函数 |
D．最小正周期为的偶函数 |
有以下四种变换方式：
① 向左平移
个单位长度，再将每个点的横坐标缩短为原来的
② 向右平移
个单位长度，再将每个点的横坐标缩短为原来的
③ 每个点的横坐标缩短为原来的，向右平移个单位长度
④ 每个点的横坐标缩短为原来的，向左平移个单位长度
其中能将
的图像变换成函数
的是（）
| A．①和③ | B．①和④ | C．②和④ | D．②和③ |
已知向量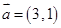
，
，
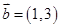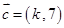，若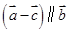
，则k =（）
| A．1 | B．3 | C．5 | D．7 |