(本小题满分13分)某工厂对一批产品的质量进行了抽样检测,右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图.已知样本中产品净重小于100克的个数是36个。
(I)求样本中净重在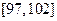 (克)的产品个数;
(克)的产品个数;
(II)若规定净重在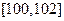 (克)的产品为一等品,依此抽样数据,求从该工厂随机抽取的3个产品中一等品个数
(克)的产品为一等品,依此抽样数据,求从该工厂随机抽取的3个产品中一等品个数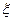 的分布列和数学期望.
的分布列和数学期望.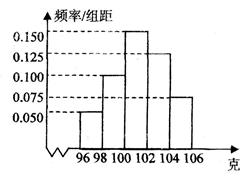
先将函数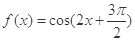 的图象上所有的点都向右平移
的图象上所有的点都向右平移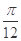 个单位,再把所有的点的横坐标都伸长为原来的2倍,纵坐标不变,得到函数
个单位,再把所有的点的横坐标都伸长为原来的2倍,纵坐标不变,得到函数 的图象.
的图象.
(1)求函数 的解析式和单调递减区间;
的解析式和单调递减区间;
(2)若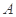 为锐角三角形的内角,且
为锐角三角形的内角,且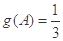 ,求
,求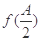 的值.
的值.
已知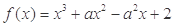 .
.
(1)若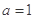 ,求曲线
,求曲线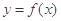 在点
在点 处的切线方程;
处的切线方程;
(2)若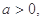 求函数
求函数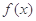 的单调区间.
的单调区间.
某公司近年来科研费用支出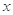 万元与公司所获得利润
万元与公司所获得利润 万元之间有如下的统计数据:
万元之间有如下的统计数据:
| x |
2 |
3 |
4 |
5 |
| Y |
18 |
27 |
32 |
35 |
(1)请根据上表提供的数据,用最小二乘法求出 关于
关于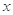 的线性回归方程
的线性回归方程 ;
;
(2)试根据(1)求出的线性回归方程,预测该公司科研费用支出为10万元时公司所获得的利润.
参考公式:用最小二乘法求线性回归方程 的系数公式:
的系数公式: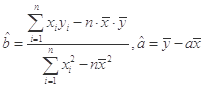
参考数据:2×18+3×27+4×32+5×35=420
设函数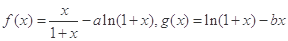 .
.
(1)若函数 在
在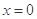 处有极值,求函数
处有极值,求函数 的最大值;
的最大值;
(2)是否存在实数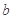 ,使得关于
,使得关于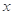 的不等式
的不等式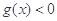 在
在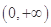 上恒成立?若存在,求出
上恒成立?若存在,求出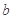 的取值范围;若不存在,说明理由;
的取值范围;若不存在,说明理由;
(3)证明:不等式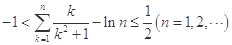 .
.
已知圆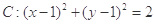 经过椭圆Γ∶
经过椭圆Γ∶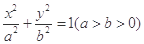 的右焦点F,且F到右准线的距离为2.
的右焦点F,且F到右准线的距离为2.
(1)求椭圆Γ的方程;
(2)过原点O的射线l与椭圆Γ在第一象限的交点为Q,与圆C的交点为P,M为OP的中点, 求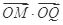 的最大值.
的最大值.