相距L＝1.5m的足够长金属导轨竖直放置，质量为m1＝1kg的金属棒ab和质量为m2＝0.27kg的金属棒cd均通过棒两端的套环水平地套在金属导轨上，如图（a）所示，虚线上方磁场方向垂直纸面向里，虚线下方磁场方向竖直向下，两处磁场磁感应强度大小相同。ab棒光滑，cd棒与导轨间动摩擦因数为μ＝0.75，两棒总电阻为1.8Ω，导轨电阻不计。ab棒在方向竖直向上，大小按图（b）所示规律变化的外力F作用下，从静止开始，沿导轨匀加速运动，同时cd棒也由静止释放。
（1）指出在运动过程中ab棒中的电流方向和cd棒受到的安培力方向；
（2）求出磁感应强度B的大小和ab棒加速度大小；
（3）已知在2s内外力F做功40J，求这一过程中两金属棒产生的总焦耳热；
（4）判断cd棒将做怎样的运动，求出cd棒达到最大速度所需的时间t0，并在图（c）中定性画出cd棒所受摩擦力fcd随时间变化的图像。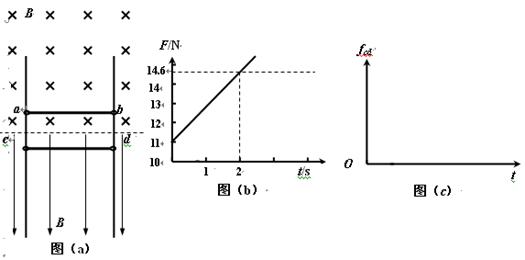
如图所示，质量分别为m1和m2的两个小球在光滑水平面上分别以速度v1、v2同向运动，并发生对心碰撞，碰后m2被右侧墙壁原速弹回，又与m1碰撞，再一次碰撞后两球都静止．求第一次碰后m1球速度的大小.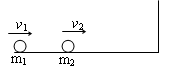
如图所示，在光滑绝缘水 平面上有两个带电小球
、
，质量分别为3m和m，小球带正电q，小球带负电-2q，开始时两小球相距s0，小球有一个水平向右的初速度v0，小球的初速度为零，若取初始状态下两小球构成的系统的电势能为零，试证明：当两小球的速度相同时系统的电势能最大，并求出该最大值；
如图所示．质量M=2kg的足够长的小平板车静止在光滑水平面上，车的一端静止着质量为MA=2kg的物体A（可视为质点）。一个质量为m=20g的子弹以500m/s的水平速度迅即射穿A后，速度变为100m/s，最后物体A静止在车上。若物体A与小车间的动摩擦因数μ=0.5（g取10m/s2。）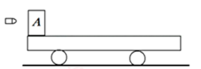
（ⅰ）平板车最后的速度是多大?
（ⅱ）全过程损失的机械能为多少?
（ⅲ）A在平板车上滑行的时间为多少?
如图所示，有n个相同的质点静止在光滑水平面上的同一直线上，相邻的两个质点间的距离都是1m，在某时刻给第一个质点一个初速度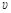
，依次与第二个、第三个…质点相碰，且每次碰后相碰的质点都粘在一起运动，求从第一个质点开始运动到与第n个质点相碰所经历的时间．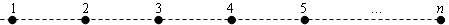
如图所示，一辆质量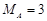
kg的小车静止在光滑的水平面上，小车上有一质量
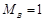kg的光滑小球，将一轻质弹簧压缩并锁定，此时弹簧的弹性势能为
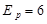J，小球脱离弹簧后与小车右壁的油灰阻挡层碰撞并被粘住，L=1.2m。求：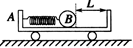
（1）小球脱离弹簧时小球和小车各自的速度；
（2）整个过程中，小车移动的距离（只要写出结果）