(本小题满分14分)椭圆E中心在原点O,焦点在x轴上,其离心率e=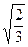 ,过点C(-1,0)的直线l与椭圆E相交于A、B两点,且C分有向线段
,过点C(-1,0)的直线l与椭圆E相交于A、B两点,且C分有向线段 的比为2.
的比为2.
(1)用直线l的斜率k(k≠0)表示△OAB的面积;
(2)当△OAB的面积最大时,求椭圆E的方程.
(本小题满分12分)
已知 关于
关于 的方程
的方程 有两个不等的负根;
有两个不等的负根; 关于
关于 的方程
的方程 无实根。若
无实根。若 为真,
为真, 为假,求
为假,求 的取值范围
的取值范围
(本小题满分14分)
已知等差数列{an}的首项为a,公差为b,等比数列{bn}的首项为b,公比为a,存在m,n∈N+使得am+1=bn成立,其中a,b均为正整数,且a1<b1<a2<b2<a3 ;
(1)求数列{an},{bn}的通项公式;
(2)设函数f(x)=bmx+bm-1x2+…+b1xm,f′(x)是函数f(x)的导函数;令Sm=f′(1),求Sm(用含n的代数式表示)
(本小题满分13分)
如图M为的△ABC的中线AD的中点,过M的直线分别与边AB,AC交于点P,Q,设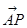 =x
=x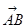 ,
,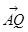 =y
=y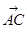 ,记y=f(x)
,记y=f(x)
(1)求函数y=f(x)的表达式;
(2)设g(x)=x3+3a2x+2a,(x∈[0,1]),若对于任意x1∈[ ,1],总存在x2∈[0,1]使得f(x1)=g(x2)成立,求实数a的取值范围;
,1],总存在x2∈[0,1]使得f(x1)=g(x2)成立,求实数a的取值范围;
(本小题满分12分)
如图,在三棱锥ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,AB=BC且AB⊥BC,O为AC中点。
(1)求直线A1C与平面A1AB所成角的正弦值;
(2)在BC1上是否存在一点E,使得OE∥平面A1AB,若不存在,说明理由;若存在,确定点E的位置.
.(本小题满分12分)
某化妆品生产企业为了占有更多的市场份额,已在2011年度进行一系列促销活动,经过市场调查和测算,化妆品的年销量x万件与年促销费t万元之间满足3-x与t+1成反比例,如果不搞促销活动,化妆品的年销量只能是1万件。已知2011年生产化妆品的设备折旧、维修等固定费用为3万元,每生产1万件化妆品需再投入32万元的生产费用。若将每件化妆品的售价定为:其生产成本的1.5倍与“平均每件促销费的一半”之和,则当年生产的化妆品正好能销完。
(1)将2011年的利润y(万元)表示为促销费t(万元)的函数
(2)该企业2011年的促销费投入多少元时,企业的年利润最大?
(注:利润=销售收入-生产成本-促销费,生产成本=固定费用+生产费用)