反射式调管是常用的微波器械之一,它利用电子团在电场中的震荡来产生微波,其震荡原理与下述过程类似。如图所示,在虚线两侧分别存在着方向相反的两个匀强电场,一带电微粒从A点由静止开始,在电场力作用下沿直线在、两点间往返运动。已知电场强度的大小分别是和,方向如图所示,带电微粒质量,带电量,A点距虚线的距离,不计带电微粒的重力,忽略相对论效应。求:
(1)点到虚线的距离;
(2)带电微粒从点运动到点所经历的时间。

如图所示,物体在15N的推力F的作用下沿水平地面向右匀速直线运动,已知物体的重力为31N,拉力为F与水平方向的夹角为θ=37°,(sin37°=0.6,cos37°=0.8)问:
(1)物体受到地面的支持力为多大
(2)物体受到的摩擦力为多大
(3)物体与地面的动摩擦因数μ
一辆汽车以某一速度沿平直公路匀速行驶10s,紧接着以大小为2m/s2的加速度匀减速行驶了10s刚好停止.求:
(1)汽车匀速行驶时的速度;
(2)汽车匀减速行驶的位移;
(3)汽车在这20s内的平均速度.
质量为30kg的小孩坐在10kg的雪橇上,大人用与水平方向成37°斜向上的大小为100N的拉力拉雪橇,使雪橇沿水平地面做匀速运动(sin37°=0.6,cos37°=0.8,g取10N/kg),求: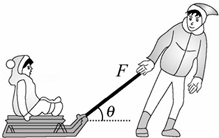
(1)地面对雪橇的支持力大小;
(2)雪橇与水平地面的动摩擦因数的大小.
如图所示,用水平力F将一个木块压在竖直墙壁上,已知木块重G=6N,木块与墙壁间的动摩擦因数μ=0.25,最大静摩擦约等于滑动摩擦力.(g=10N/kg)问:
(1)当F=30N时,木块受到的摩擦力为多大?
(2)当F增大为40N时,木块受到的摩擦力为多大?
(3)当F=10N时,此时木块受到的摩擦力为多大?
(4)当物体在下滑过程中撤去F时,木块受到的摩擦力又为多大?
在一长直赛道上,有一辆赛车前方300m处有一安全车正以20m/s的速度匀速前进,这时赛车从静止出发以2m/s2的加速度追赶.求:
(1)赛车出发3s末的速度多大?
(2)赛车何时追上安全车?
(3)赛车追上安全车之前最远相距多少米?