为了探测星球,载着登陆舱的探测飞船在以该星球中心为圆心,半径为的圆轨道上运动,周期为。总质量为。随后登陆舱脱离飞船,变轨到离星球更近的半径为的圆轨道上运动,此时登陆舱的质量为则()
| A. | 星球的质量为 |
| B. | 星球表面的重力加速度为 |
| C. | 登陆舱在 与 轨道上运动时的速度大小之比为 |
| D. | 登陆舱在半径为 轨道上做圆周运动的周期为 |
如图所示电路中,L为自感系数很大的电感线圈,其直流电阻不计,A、B为两相同灯泡,则下列说法正确的是()
A.合上S的瞬间,A、B同时亮
B.合上S的瞬间,A先亮,B后亮
C.合上S后,A逐渐变得更亮,B逐渐变暗直至熄灭
D.断开S时,A立即熄灭,B灯重新亮随后逐渐熄灭
如图所示,单匝线圈ABCD在外力作用下以速度v向右匀速进入匀强磁场,第二次又以速度2v匀速进入同一匀强磁场.则:第二次进入与第一次进入时()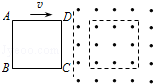
| A.线圈中电流之比为1:1 |
| B.外力做功的功率之比为4:1 |
| C.线圈中产生热量之比为2:1 |
| D.通过导线横截面电荷量之比为2:1 |
竖直放置的线圈固定不动,将磁铁从线圈上方插入或拔出,线圈和电流表构成的闭合回路中就会产生感应电流,下列各图中分别标出了磁铁的极性、磁铁相对线圈的运动方向以及线圈中产生的感应电流的方向等情况,其中图示正确的是()
A.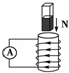 |
B. |
C. |
D. |
一矩形线圈位于一个方向垂直线圈平面向里的磁场中,如图1所示,磁感应强度B随t的变化规律如图2所示.以I表示线圈中的感应电流,以图1线圈上箭头所示方向的电流为正,则以下的i﹣t图中正确的是()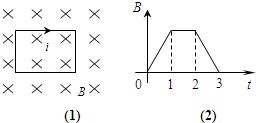
A. |
B.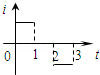 |
C.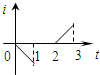 |
D.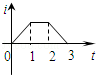 |
如图所示,边长为L的正方形导线框其质量为m,在距磁场上边界高H处自由下落,其下边框ab进入匀强磁场后,线圈开始做减速运动,直到其上边框cd刚穿出磁场时,其速度减为ab边刚进入磁场时的一半,磁场的宽度也为L,则线框穿越匀强磁场过程中产生的焦耳热为()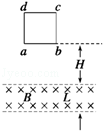
| A.2mgL | B.2mgL+mgH | C.2mgL+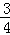 mgH mgH |
D.2mgL+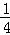 mgH mgH |