已知正方形的中点为直线 和
和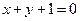 的交点,正方形一边所在直线的方程为
的交点,正方形一边所在直线的方程为 ,求其他三边所在直线的方程.
,求其他三边所在直线的方程.
几何体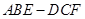 的三视图如图,
的三视图如图, 与
与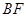 交于点
交于点 ,
,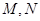 分别是直线
分别是直线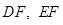 的中点,
的中点,
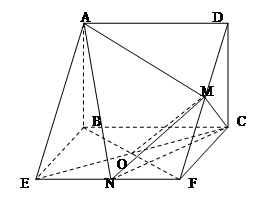
(I) 面
面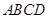 ;
;
(II)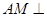 面
面 ;
;
(Ⅲ)求二面角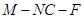 的平面角的余弦值.
的平面角的余弦值.
已知函数 (
(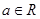 )在
)在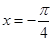 取到极值,
取到极值,
(I)写出函数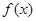 的解析式;
的解析式;
(II)若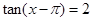 ,求
,求 的值;
的值;
(Ⅲ)从区间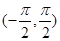 上的任取一个
上的任取一个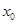 ,若
,若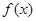 在点
在点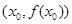 处的切线的斜率为
处的切线的斜率为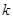 ,求
,求 的概率.
的概率.
已知椭圆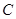 :
: (
( )的短轴长与焦距相等,且过定点
)的短轴长与焦距相等,且过定点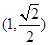 ,倾斜角为
,倾斜角为 的直线
的直线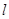 交椭圆
交椭圆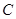 于
于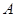 、
、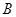 两点.
两点.
(Ⅰ)求椭圆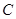 的方程;
的方程;
(Ⅱ)确定直线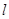 在
在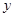 轴上截距的范围.
轴上截距的范围.
投掷一枚均匀硬币2次,记2次都是正面向上的概率为 ,恰好
,恰好 次正面向上的概率为
次正面向上的概率为 ;等比数列
;等比数列 满足:
满足: ,
,
(I)求等比数列 的通项公式;
的通项公式;
(II)设等差数列 满足:
满足: ,
, ,求等差数列
,求等差数列 的前
的前 项和
项和 .
.
如图,已知直线l:y=2x-4交抛物线y2=4x于A,B两点,试在抛物线AOB这段曲线上求一点P,使△PAB的面积最大,并求出这个最大面积.