通过随机询问110名不同的大学生是否爱好某项运动,得到如下的列联表:
| 男 |
女 |
总计 |
|
| 爱好 |
40 |
20 |
60 |
| 不爱好 |
20 |
30 |
50 |
| 总计 |
60 |
50 |
110 |
由
附表:
| 0.050 |
0.010 |
0.001 |
|
| 3.841 |
6.635 |
10.828 |
参照附表,得到的正确结论是()
| A. | 有99%以上的把握认为"爱好该项运动与性别有关" |
| B. | 有99%以上的把握认为"爱好该项运动与性别无关" |
| C. | 在犯错误的概率不超过0.1%的前提下,认为"爱好该项运动与性别有关" |
| D. | 在犯错误的概率不超过0.1%的前提下,认为"爱好该项运动与性别无关" |
 内有任意三点不共线的2006个点,加上A、B、C三个顶点,共2009个点,把这2009个点连线形成互不重叠的小三角形,则一共可以形成小三角形的个数为()
内有任意三点不共线的2006个点,加上A、B、C三个顶点,共2009个点,把这2009个点连线形成互不重叠的小三角形,则一共可以形成小三角形的个数为()
(A) (B)4010(C)4011(D)4013
(B)4010(C)4011(D)4013
已知随机变量 服从二项分布,即
服从二项分布,即 ,则
,则 的值为()
的值为()
A. |
B. |
C. |
D. |
四张卡片上分别写有“荣”、“八”、“耻”、“八”四个汉字,一个不识字的幼儿随机地把它们排成一排,刚好排成“八荣八耻”的概率是()
A. |
B. |
C. |
D. |
已知 ,且
,且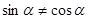 ,则向量
,则向量 与
与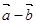 的夹角是( )
的夹角是( )
| A.0° | B.30° | C.60° | D.90° |
若一条直线与平面成45°角,则该平面内与此直线成30°角的直线的条数是()
| A.0 | B.1 | C.2 | D.3 |