有甲、乙、丙、丁四位歌手参加比赛,其中只有一位获奖,有人走访了四位歌手,甲说:“是乙或丙获奖”,乙说:“甲、丙都未获奖”,丙说:“我获奖了”,丁说:“是乙获奖”。四位歌手的话只有两名是对的,则获奖的歌手是( )
| A.甲 | B.乙 | C.丙 | D.丁 |
设 ,则“
,则“ ” 是“
” 是“ 且
且 ”的()
”的()
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.即不充分也不必要条件 |
设复数 (其中
(其中 为虚数单位),则
为虚数单位),则 的虚部为()
的虚部为()
A. |
B. |
C. |
D. |
已知集合 ,
, ,如果
,如果 ,则
,则 等于 ()
等于 ()
A. |
B. |
C. 或 或 |
D. |
计算机考试分理论考试与实际操作考试两部分进行,每部分考试成绩只记“合格”与“不合格”,两部分考试都“合格”者,则计算机考试“合格“并颁发”合格证书“.甲、乙、丙三人在理论考试中“合格”的概率依次为 ,在实际操作考试中“合格”的概率依次为
,在实际操作考试中“合格”的概率依次为 ,所有考试是否合格相互之间没有影响。
,所有考试是否合格相互之间没有影响。
(1)假设甲、乙、丙3人同时进行理论与实际操作两项考试,谁获得“合格证书”的可能性大?
(2)求这3人进行理论与实际操作两项考试后,恰有2人获得“合格证书”的概率;
(3)用X表示甲、乙、丙3人计算机考试获“合格证书”的人数,求X的分布列和数学期望EX。
定义在R上的函数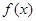 满足
满足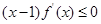 ,且
,且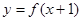 为偶函数,当
为偶函数,当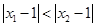 时,有()
时,有()
A.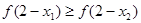 |
B.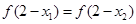 |
C.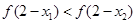 |
D.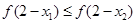 |