如下图甲所示是某同学设计的一种振动发电装置的示意图，它的结构是一个套在辐向形永久磁铁槽中的半径为r＝0.10 m、匝数n＝20匝的线圈，磁场的磁感线均沿半径方向均匀分布(其右视图如下图乙所示)．在线圈所在位置磁感应强度B的大小均为B＝ T，线圈的电阻为R1＝0.50 Ω，它的引出线接有R2＝9.5 Ω的小电珠L.外力推动线圈框架的P端，使线圈沿轴线做往复运动，便有电流通过小电珠．当线圈运动速度v随时间t变化的规律如下图丙所示时(摩擦等损耗不计)．求：
(1)小电珠中电流的最大值；
(2)电压表的示数；
(3)t＝0.1 s时外力F的大小；
(4)在不改变发电装置结构的条件下，要使小电珠的功率提高双倍，可采取什么办法(至少说出两种方法)?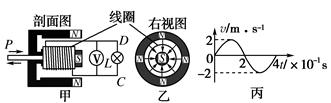
如图所示，质量为mB=14kg的木板B放在水平地面上，质量为mA=10kg的木箱A放在木板B上。一根轻绳一端拴在木箱上，另一端拴在地面的木桩上，绳绷紧时与水平面的夹角为θ=37°。已知木箱A与木板B之间的动摩擦因数μ1=0.5，木板B与地面之间的动摩擦因数μ2=0.4。重力加速度g取10m/s2。现用水平力F将木板B从木箱A下面匀速抽出，试求：（sin37°=0.6，cos37°=0.8）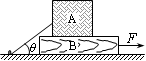
（1）绳上张力FT的大小；
（2）拉力F的大小。
如图，水平地面上静止放置着物块B和C，相l＝1.0 m，物块A以速度
＝10 m/s沿水平方向与B正碰．碰撞后A和B牢固地粘在一起向右运动，并再与C发生正碰，碰后瞬间C的速度v="2.0" m/s.已知A和B的质量均为m，C的质量为A质量的k倍，物块与地面的动摩擦因数μ=0.45.（设碰撞时间很短，g取10 m/s2）
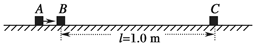
（1）计算与C碰撞前瞬间AB的速度；
（2）根据AB与C的碰撞过程分析k的取值范围，并讨论与C碰撞后AB的可能运动方向．
如图所示，质量为m的铅弹以大小为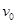
初速度射入一个装有砂子的总质量为M的静止的砂车中并与车相对静止，砂车与水平地面间的摩擦可以忽略．求：
（1）弹和砂车的共同速度；
（2）弹和砂车获得共同速度后，砂车底部出现一小孔，砂子从小孔中流出，当漏出质量为
的砂子时砂车的速度
一个质子和两个中子聚变成一个氚核，已知质子质量为1.0073u，中子质量为1.0087u，氚核质量为3.0180u，
（1）写出核反应方程；（2）求该反应中释放的核能。
如图所示，用长为L的细线一端系住质量为m的小球，另一端固定在A点，AB是过A的竖直线，E为AB上的一点，且AE=0.5L，过E作水平线EF，在EF上可以钉铁钉D，现将细线水平拉直，然后小球由静止释放。不计一切摩擦，不计线与钉子碰撞时的能量损失，求：
（1）若无铁钉D，小球运动到最低点B时细线的拉力TB=?
（2）若钉上铁钉D且线拉力足够大，使小球恰能绕钉子在竖直面内做完整圆周运动，则钉子D 与点E 距离DE=？
（3）钉铁钉D后，若线能承受的最大拉力是9mg，小球能绕钉子在竖直面内做完整圆周运动，ED取值范围是多少？