如图所示,一绝缘细圆环半径为r,环面处于竖直平面内,场强为E的水平匀强电场与圆环平面平行。环上穿有一电量为+q、质量为m的小球,可沿圆环做无摩擦的圆周运动。电场力大小等于重力,重力加速度为g,若小球能完成完整的圆周运动,则
(1)小球经水平直径左端A点时的速度大小vA是多大?
(2)当小球运动到圆环的最低点B点时,速度又是多大?此时小球对圆环的作用力是多少?
水平放置的轻弹簧左端固定,小物块P(可视为质点)置于水平桌面的A点并与弹簧的右端接触但不相连,此时弹簧处于原长,现用力缓慢地向左水平推P至B点(弹簧仍在弹性限度内),推力做的功是6J,撤去推力后,P沿桌面滑到一辆停在光滑水平地面、紧靠水平桌边缘的平板小车Q上,小车的上表面与桌面在同一水平面上,已知P的质量为m=1kg,Q的质量为M=4kg,A、B间距L1=20cm,A离桌边沿C的距离L2=60cm,P与桌面间的动摩擦因数为μ1=0.4,g=10m/s2,物块P滑出小车Q时的速度υ1=0.8m/s,小车Q长L3=50cm.求:
(1)小物块P在桌边沿C的速度大小υc=?
(2)小物块P与小车Q上表面间的动摩擦因数μ2=?
(3)小物块P在小车上表面上运动的过程中,小车通过的距离?
如图所示,滑块的质量M=2kg,开始静止在水平面上的A点,滑块与水平面间的摩擦因数为μ=0.2,与A点相距S=2.25m的B点上方有一质量m=1.2kg的小球,小球被一长为l=0.5米的轻绳挂在O点而处于静止状态。现给滑块一瞬时冲量I=10N・S,让滑块沿水平面向右运动,此后与小球发生碰撞,碰后小球恰能在竖直平面内完成完整的圆周运动(g=10m/s2)。求: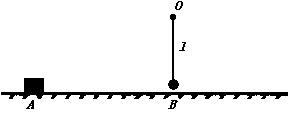
(1)滑块最终静止在距离A点多远处?
(2)因滑块与小球碰撞而损失的机械能是多少?
如图所示,真空中金属板M、N相距为d,当N板用波长为λ的光照射时,电路中的电流恒为I.设电子的电荷量为e,质量为m,真空中光速为c.
(1)求每秒到达M板的电子数.
(2)当垂直于纸面再加一匀强磁场,且磁感应强度为B时,电路中的电流恰好为零,求从N板逸出光电子的最大初动能和N板的逸出功.
如图12所示质量为M的小物块A静止在离地面高h的水平桌面的边缘,质量为m的小物块B沿桌面向A运动并以速度v0与之发生正碰(碰撞时间极短)。碰后A离开桌面,其落点离出发点的水平距离为L。碰后B反向运动。已知B与桌面的动摩擦因数为μ,重力加速度为g,桌面足够长。求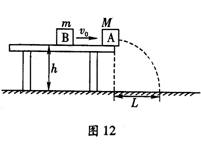
(1)碰后A、B小物块分离的瞬间速率各是多少?
(2)碰后小物块B后退的最大距离是多少?
一人用一根长L=1m,最大只能承受T=46N拉力的轻绳子,拴着一个质量m=1kg的小球(不考虑其大小),在竖直平面内作圆周运动,已知圆心O离地高H=21m,如图7所示,若小球运动到达最低点时绳刚好被球拉断,求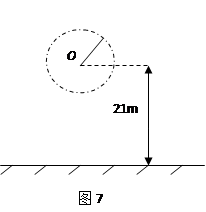
(1)小球到达最低点的速度大小是多少?
(2)小球落地点到O点的水平距离是多少?(g=10m/s2)