如图,用与底面成 角的平面截圆柱得一椭圆截线,则该椭圆的离心率为 ( )
角的平面截圆柱得一椭圆截线,则该椭圆的离心率为 ( ) A.
A. B.
B.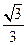 C.
C. D.非上述结论
D.非上述结论
命题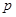 :存在实数
:存在实数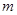 ,使方程
,使方程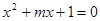 有实数根,则“非
有实数根,则“非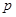 ”形式的命题是()
”形式的命题是()
A.存在实数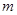 ,使得方程 ,使得方程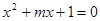 无实根 无实根 |
B.不存在实数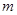 ,使得方程 ,使得方程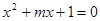 有实根 有实根 |
C.对任意的实数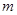 ,使得方程 ,使得方程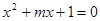 有实根 有实根 |
D.至多有一个实数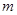 ,使得方程 ,使得方程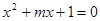 有实根 有实根 |
复数 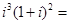 ()
()
| A.2 | B.-2 | C.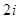 |
D.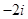 |
若直线 与圆
与圆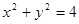 没有交点,则过点
没有交点,则过点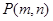 的直线与椭圆
的直线与椭圆 的公共点个数为( )
的公共点个数为( )
| A.至少一个 | B.0个 | C.1个 | D.2个 |
设M( ,
,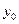 )为抛物线C:
)为抛物线C: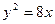 上一点,F为抛物线C的焦点,以F为圆心、
上一点,F为抛物线C的焦点,以F为圆心、 为半径的圆和抛物线C的准线相交,则
为半径的圆和抛物线C的准线相交,则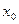 的取值范围是( )
的取值范围是( )
| A.[2,+∞) | B.(2,+∞) | C.(0,2) | D.[0,2] |
已知椭圆 (
(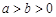 )与双曲线
)与双曲线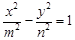 (
( ,
, )有相同的焦点
)有相同的焦点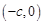 和
和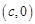 ,若
,若 是
是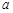 、
、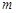 的等比中项,
的等比中项,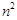 是
是 与
与 的等差中项,则椭圆的离心率是()
的等差中项,则椭圆的离心率是()
A.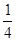 |
B. |
C.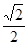 |
D.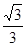 |