设V是全体平面向量构成的集合,若映射 满足:对任意向量 ,
以及任意 ,均有 则称映射 具有性质 .现给出如下映射:
①
②
③ .
其中,具有性质 的映射的序号为.(写出所有具有性质P的映射的序号)
一个棱锥的三视图如图所示,则这个棱锥的体积为________.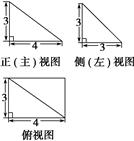
若圆C的半径为1,圆心在第一象限,且与直线4x-3y=0和x轴相切,则该圆的标准方程是________.
下面四个命题:
①已知函数f(x)=sin x,在区间[0,π]上任取一点x0,则使得f(x0)>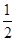 的概率为
的概率为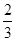 ;
;
②函数y=sin 2x的图象向左平移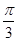 个单位得到函数y=sin
个单位得到函数y=sin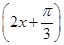 的图象;
的图象;
③命题“∀x∈R,x2-x+1≥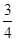 ”的否定是“∃x0∈R,x02-x0+1<
”的否定是“∃x0∈R,x02-x0+1<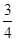 ”;
”;
④若函数f(x)是定义在R上的奇函数,则f(x+4)=f(x),则f(2 012)=0.
其中所有正确命题的序号是________.
抛物线y=2x2的准线方程是________.
向量a=(-1,1)在向量b=(3,4)方向上的投影为________.