今年我省干旱灾情严重,甲地急需要抗旱用水15万吨,乙地13万吨.现有A、B两水库各调出14万吨水支援甲、乙两地抗旱.从A地到甲地50千米,到乙地30千米;从B地到甲地60千米,到乙地45千米.
⑴设从A水库调往甲地的水量为x万吨,完成下表

|
甲 |
乙 |
总计 |
||||||
| A |
x |
|
14 |
||||||
| B |
|
|
14 |
||||||
| 总计 |
15 |
13 |
28 |
⑵请设计一个调运方案,使水的调运量尽可能小.(调运量=调运水的重量×调运的距离,单位:万吨•千米)
如图,用长为32米的篱笆围成一个外形为矩形的花圃,花圃的一边利用原有墙,中间用2道篱笆割成3个小矩形.已知原有墙的最大可利用长度为15米,花圃的面积为S平方米,平行于原有墙的一边BC长为x米.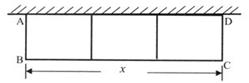
(1)求S关于x的函数关系式;
(2)当围成的花圃面积为60平方米时,求AB的长;
(3)能否围成面积比60平方米更大的花圃?如果能,那么最大的面积是多少?如果不能,请说明理由.
如图,正比例函数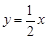 的图象与反比例函数
的图象与反比例函数 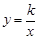
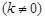 在第一象限的图象交于
在第一象限的图象交于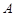 点,过
点,过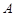 点作
点作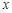 轴的垂线,垂足为
轴的垂线,垂足为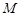 ,已知
,已知 的面积为1.
的面积为1.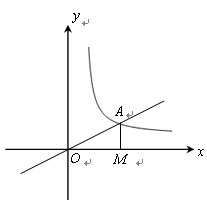
(1)求反比例函数的解析式;
(2)当x>0时,根据图象直接写出不等式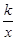 >
>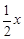 的解;
的解;
(3)如果 为反比例函数在第一象限图象上的点(点
为反比例函数在第一象限图象上的点(点 与点
与点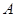 不重合),且
不重合),且 点的横坐标为1,在
点的横坐标为1,在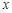 轴上求一点
轴上求一点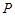 ,使
,使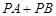 最小.
最小.
如图,已知AB是⊙O的弦,OB=2,∠B=30°,C是弦AB上一点(不与点A、B重合),连结CO并延长CO交⊙O于点D,连结AD.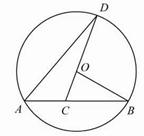
(1)求弦长AB的长度;(结果保留根号);
(2)当∠D=20°时,求∠BOD的度数.
已知抛物线y=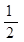 x2+x-
x2+x-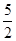 .
.
(1)求它的顶点坐标和对称轴;
(2)若该抛物线与x轴的两个交点为A、B,求线段AB的长.
已知反比例函数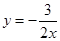
(1)直接写出这个函数的比例系数____________;
(2)求当x=-10时函数y的值;
(3)求当y=6时自变量x的值.