如图6．点D，E在△ABC的边BC上．连接AD．AE．①AB=AC：②AD=AE：
③BD=CE。以此三个等式中的两个作为命题的题设，另一个作为命题的结论．构成三个命题：①②
③；①③②，②③①。
（1）以上三个命题是真命题的为(直接作答)__________________；
（2）选择一个真命题进行证明(先写出所选命题．然后证明)。
（1）计算：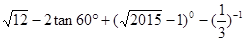
；
（2）化简：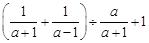
．
如图，抛物线y=ax2+bx（a＞0）与双曲线y=
相交于点A，B．已知点B的坐标为（﹣2，﹣2），点A在第一象限内，且tan∠AOx=4．过点A作直线AC∥x轴，交抛物线于另一点C．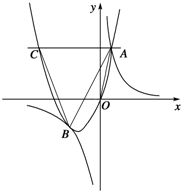
（1）求双曲线和抛物线的解析式；
（2）计算△ABC的面积；
（3）在抛物线上是否存在点D，使△ABD的面积等于△ABC的面积．若存在，请你写出点D的坐标；若不存在，请你说明理由．
如图，在矩形ABCD中，AD=4，AB=m（m＞4），点P是AB边上的任意一点（不与A、B重合），连结PD，过点P作PQ⊥PD，交直线BC于点Q．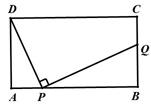
（1）当m=10时，是否存在点P使得点Q与点C重合？若存在，求出此时AP的长；若不存在，说明理由；
（2）连结AC，若PQ∥AC,求线段BQ的长（用含m的代数式表示）
（3）若△PQD为等腰三角形，求以P、Q、C、D为顶点的四边形的面积S与m之间的函数关系式，并写出m的取值范围．
如图，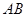
是
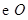的直径，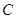
为圆周上一点，
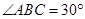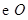，过点
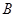的切线与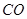
的延长线交于点
．
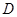求证：（1）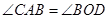
；
（2）
≌
．
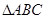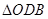刘大叔去年承包了10亩地种植甲、乙两种蔬菜，共获利18000元，其中甲种蔬菜每亩获利2000元，乙种蔬菜每亩获利1500元，刘大叔去年甲、乙两种蔬菜各种植了多少亩？