如图所示，质量为m的物体(可视为质点)以某一速度从A点冲上倾角为30°的固定斜面，其运动的加速度大小为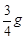
，此物体在斜面上上升的最大高度为h，则在这个过程中物体
A．重力势能增加了 mgh |
B．克服摩擦力做功 mgh |
C．动能损失了 mgh |
D．机械能损失了 |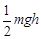
A、B两球在光滑水平面上做相向运动，已知mA>mB，当两球相碰后.其中一球停止，则可以断定（ ）
| A．碰前A的动量等于B的动量 |
| B．碰前A的动量大于B的动量 |
| C．若碰后A的速度为零，则碰前A的动量大于B的动量 |
| D．若碰后B的速度为零，则碰前A的动量小于B的动量 |
如图16-4-3所示在质量为M的小车挂有一单摆，摆球的质量为m0，小车和单摆以恒定的速度v沿光滑水平地面运动，与位于正对面的质量为m的静止木块发生碰撞，碰撞的时间极短，在此碰撞过程中，下列哪个或哪些情况的说法是可能发生的（）
图16-4-3
| A．小车、木块、摆球的速度都发生变化，分别变为v1、v2、v3，满足(M+m0)v=Mv1+mv2+m0v3 |
| B．摆球的速度不变，小车和木块的速度变为v1和v2，满足Mv=Mv1+mv2 |
| C．摆球的速度不变，小车和木块的速度都变为v1, Mv=(M+m)v1 |
| D．小车和摆球的速度都为v1，木块的速度变为v2，满足(M+m0)v=(M+m0)v1+mv2. |
如图16-4-5所示，长木板ab的b端固定一挡板，木板连同挡板的质量为M="4.0" kg，a、b间距离s="2.0" m.木板位于光滑水平面上.在木板a端有一小物块，其质量m="1.0" kg，小物块与木板间的动摩擦因数μ=0.10，它们都处于静止状态.现令小物块以初速度v0="4.0" m/s沿木板向前滑动，直到和挡板相撞.碰撞后，小物块恰好回到a端而不脱离木板.求碰撞过程中损失的机械能.
图16-4-5
第一个粒子质量是m1，以v0的速度与原来静止的质量为m2的第二个粒子发生一维碰撞.测出了碰撞后第二个粒子的速度为v2,求第一个粒子原来速度v0的值可能范围.
如图16-4-4所示，有两个质量相同的小球A和B（大小不计），A球用细绳吊起，细绳长度等于悬点距地面的高度，B点静止放于悬点正下方的地面上，现将A球拉到距地面高度为h处由静止释放，摆动到最低点与B球碰撞后粘在一起共同上摆，则它们升起的最大高度为（ ）
图16-4-4
| A．h/2 | B．h |
| C．h/4 | D． |