如图，在平面直角坐标系中，O为坐标原点，P是反比例函数
y＝
（x＞0）图象上的任意一点，以P为圆心，PO为半径的圆与x、y轴分别交于点A、
B．
（1）判断P是否在线段AB上，并说明理由；
（2）求△AOB的面积；
（3）Q是反比例函数y＝（x＞0）图象上异于点P的另一点，请以Q为圆心，QO
半径画圆与x、y轴分别交于点M、N，连接AN、MB．求证：AN∥MB．
 |
已知AB是⊙O的直径，AP是⊙O的切线，A是切点，BP与⊙O交于点C．
(1)如图①，若AP＝6，PC＝4，求圆的半径（结果保留根号）；
(2)如图②，若D为AP的中点，求证：直线CD是⊙O的切线．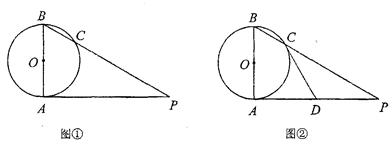
某居民小区一处圆柱形的输水管道破裂，维修人员为更换管道，需确定管道圆形截面的半径．下图是水平放置的破裂管道有水部分的截面．
(1)作图题：请你用圆规、直尺作出这个输水管道的圆形截面的圆心；（不写作法，保留作图痕迹）
(2)若这个输水管道有水部分的水面宽AB＝8，水面最深的地方的高度为2，求这个圆形截面的半径．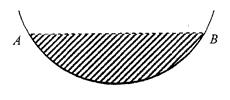
已知关于x的方程k2x2＋(2k－1)x＋1＝0有两个实数根x1、x2
(1)求k的取值范围；
(2)是否存在k的值，可以使得这两根的倒数和等于0？如果存在，请求出k，若不存在，请说明理由．
解方程组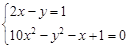
解下列分式方程：
(1)
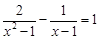； (2)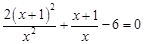
．