如图,在Rt△ABC中,∠B=90°,AB=1,BC= ,以点C
,以点C
为圆心,CB为半径的弧交CA于点D;以点A为圆心,AD为半径的弧交AB于点E.
(1)求AE的长度;
(2)分别以点A、E为圆心,AB长为半径画弧,两弧交于点F(F与C在AB两侧),连接AF、EF,设EF交弧DE所在的圆于点G,连接AG,试猜想∠EAG的大小,并说明理由.
 |
如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.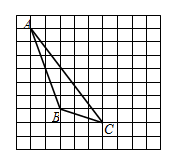
(1)画出△ABC向右平移4个单位后得到的△A1B1C1;
(2)图中AC与A1C1的关系是:;
(3)画出△ABC中AB边上的中线CD;
(4)△ACD的面积为.
先化简,再求值: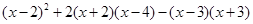 ,其中
,其中 .
.
(1)如图1,a∥b,则∠1+∠2=
(2)如图2,AB∥CD,则∠1+∠2+∠3=,并说明理由
(3)如图3,a∥b,则∠1+∠2+∠3+∠4=
(4)如图4,a∥b,根据以上结论,试探究∠1+∠2+∠3+∠4+…+∠n=(直接写出你的结论,无需说明理由)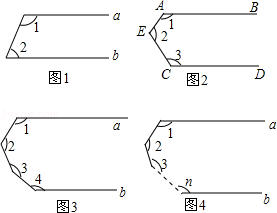
如图,将三角形ABC向右平移5个单位长度,再向上平移3个单位长度请回答下列问题:
(1)平移后的三个顶点坐标分别为:A1,B1,C1;
(2)画出平移后三角形A1B1C1;
(3)求三角形ABC的面积.
完成下面证明: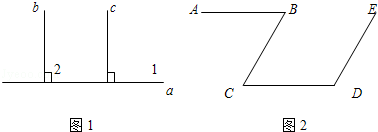
(1)如图1,已知直线b∥c,a⊥c,求证:a⊥b
证明:∵a⊥c( 已知 )
∴∠1=( 垂直定义)
∵b∥c (已知 )
∴∠1=∠2()
∴∠2=∠1=90° ()
∴a⊥b( )
(2)如图2:AB∥CD,∠B+∠D=180°,求证:CB∥DE
证明:∵AB∥CD (已知)
∴∠B=()
∵∠B+∠D=180° (已知)
∴∠C+∠D=180° ()
∴CB∥DE()