.已知:如图4,在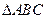 中,∠BAC=90°,DE、DF是
中,∠BAC=90°,DE、DF是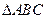 的中位线,连结EF、AD. 求证:EF=AD.
的中位线,连结EF、AD. 求证:EF=AD.
(1)如图1,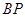 为
为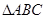 的角平分线,
的角平分线,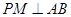 于
于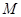 ,
,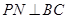 于
于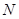 ,
,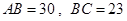 ,请补全图形,并求
,请补全图形,并求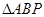 与
与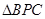 的面积的比值;
的面积的比值;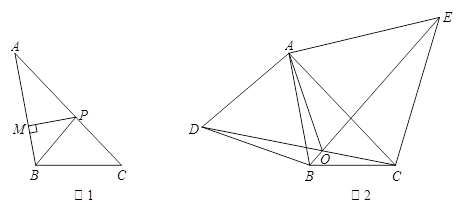
(2)如图2,分别以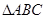 的边
的边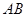 、
、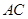 为边向外作等边三角形
为边向外作等边三角形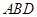 和等边三角形
和等边三角形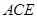 ,
,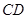 与
与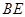 相交于点
相交于点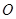 ,判断
,判断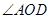 与
与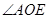 的数量关系,并证明;
的数量关系,并证明;
(3)在四边形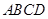 中,已知
中,已知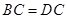 ,且
,且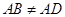 ,对角线
,对角线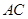 平分
平分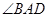 ,
,
请直接写出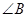 和
和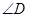 的数量关系.
的数量关系.
已知直线 经过点
经过点 、
、 .
.
(1)求直线 的解析式;
的解析式;
(2)当 时,求
时,求 的取值范围;
的取值范围;
(3)我们将横坐标、纵坐标均为整数的点称为整数点.直接写出此直线与两坐标轴围成的三角形的内部(不包含边界)的整数点的坐标.
作图题(要求:画出图形,保留作图痕迹,并简要说明画法,不要求证明).
已知∠AOB及其内部一点P.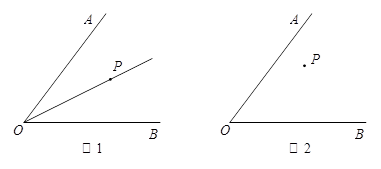
(1) 如图1,若点P在∠AOB的角平分线上,请你在图1中过点P作直线,分别交OA、OB于点C、D,使△OCD为等腰三角形,且CD是底边;
(2)若点P不在∠AOB的角平分线上(如图2),请你在图2中过点P作直线,分别交OA、OB于点C、D,使△OCD为等腰三角形,且CD是底边.
如图,点 是等边三角形
是等边三角形 内一点,且
内一点,且 ,
, 外一点
外一点 满足
满足 ,
, 平分
平分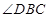 ,求
,求 的度数.
的度数.
王老师家在商场与学校之间,离学校1千米,离商场2千米.元旦前王老师骑车到商场买奖品后再到学校,结果比平常步行直接到校迟20分钟.已知骑车速度为步行速度的2.5倍,买奖品时间为10分钟,求骑车的速度.