已知:AB是⊙O的直径,弦CD⊥AB于点G,E是直线AB上一动点(不与点A、B、G重合),直线DE交⊙O于点F,直线CF交直线AB于点P.设⊙O的半径为r.
(1)如图1,当点E在直径AB上时,试证明:OE·OP=r2
(2)当点E在AB(或BA)的延长线上时,以如图2点E的位置为例,请你画出符合题意的图形,标注上字母,(1)中的结论是否成立?请说明理由.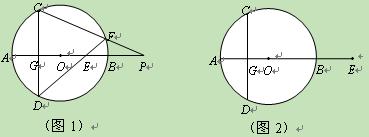
如图,点C,D在线段AB上,△PCD是等边三角形,且∠APB=1200,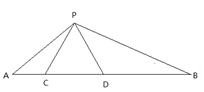
求证(1)△ACP∽△PDB,
(2)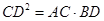
如图在正方形ABCD中,E是CD上一点,F是CB延长线上一点,且DE=BF,AF,AE之间有怎样的关系?请说明理由。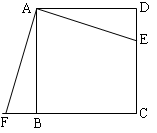
如图,△ABC为直角三角形,∠ACB=90°,CD⊥AB于D,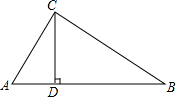
(1)找出图中所有的相似三角形,分别是 ;
(2)求证: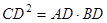
某工厂今年3月份的产值为100万元,由于受国际金融风暴的影响,5月份的产值下降到81万元,求平均每月产值下降的百分率.
甲、乙两同学只有一张乒乓球比赛的门票,谁都想去,最后商定通过转盘游戏决定.游戏规则是:转动下面平均分成三个扇形且标有不同颜色的转盘,转盘连续转动两次,若指针前后所指颜色相同,则甲去;否则乙去.(如果指针恰好停在分割线上,那么重转一次,直到指针指向一种颜色为止)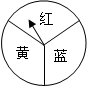
(1)转盘连续转动两次,指针所指颜色共有几种情况?通过画树状图或列表法加以说明;
(2)你认为这个游戏公平吗?请说明理由.