一宇宙空间探测器从某一星球的表面垂直升空,假设探测器的质量恒为1500kg,发动机的推力为恒力,宇宙探测器升空到某一高度时,发动机突然关闭,如图表示其速度随时间的变化规律
(1)升高6s、20s、40s,探测器的运动情况如何?(要求有计算过程,说清加速度和速度的具体值)
(2 ) 求探测器在该行星表面达到的最大高度
(3)计算该行星表面的重力加速度及发动机的推力(假设行星表面没有空气阻力)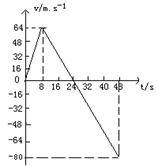
(9分)如图所示,质量为m=lkg的小物块由静止轻轻放在水平匀速运动的传送带上,从A点随传送带运动到水平部分的最右端B点,经半圆轨道C点沿圆弧切线进入竖直光滑的半圆轨道,恰能做圆周运动。C点在B点的正上方,D点为轨道的最低点。小物块离开D点后,做平抛运动,恰好垂直于倾斜挡板打在挡板跟水平面相交的E点。已知半圆轨道的半径R=0.9 m,D点距水平面的高度h =0.75 m,取g="10" m/s2,试求:
(1)摩擦力对物块做的功;
(2)小物块经过D点时对轨道压力的大小;
(3)倾斜挡板与水平面间的夹角θ。
(9分)如图,质量为2m 的物体A经一轻质弹簧与下方地面上的质量为3m 的物体B相连,弹簧的劲度系数为k,A、B都处于静止状态.一条不可伸长的轻绳绕过定滑轮,一端连物体A,另一端连一轻挂钩.开始时各段绳都处于伸直状态,A上方的一段绳沿竖直方向.现在挂钩上挂一质量为2.5m 的物体C并从静止状态释放,已知它恰好能使B离开地面但不继续上升,已知重力加速度为g.试求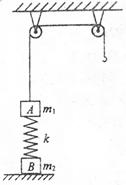
(1)物体C下降到速度最大时,地面对B的支持力多大?
(2)物体C下降的最大距离;
(3)物体C在最低点时,轻绳的拉力是多大?
(8分)在一次宇宙探险活动中,发现一行星,经观测其半径为R,当飞船在接近行星表面的上空做匀速圆周运动时,周期为T飞船着陆后,宇航员用绳子拉着质量为m的仪器箱在平坦的“地面”上运动,已知拉力大小为F,拉力与水平面的夹角为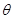 ,箱子做匀速直线运动.(引力常量为G)求:
,箱子做匀速直线运动.(引力常量为G)求:
(1)行星的质量M;
(2)箱子与“地面”间的动摩擦因数
(8分)一物体做匀减速直线运动,一段时间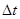 (未知)内通过的位移为
(未知)内通过的位移为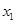 ,紧接着的
,紧接着的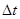 时间内通过的位移为
时间内通过的位移为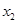 ,此时,物体仍然在运动,求再经过多少位移物体速度刚好减为零。
,此时,物体仍然在运动,求再经过多少位移物体速度刚好减为零。
如图所示,在空中 点将质量为
点将质量为 的小球以某一水平速度抛出,将无碰撞地由
的小球以某一水平速度抛出,将无碰撞地由 点进入竖直平面内半径
点进入竖直平面内半径 的内壁光滑圆管弧形轨道,然后经最低点
的内壁光滑圆管弧形轨道,然后经最低点 无能量损失地进入足够长光滑水平轨道,与另一静止的质量为
无能量损失地进入足够长光滑水平轨道,与另一静止的质量为 小球发生碰撞并粘连在一起(不再分开)压缩弹簧,弹簧左端与小球M栓接,弹簧右端与固定挡板栓接。已知圆管的直径远小于轨道半径
小球发生碰撞并粘连在一起(不再分开)压缩弹簧,弹簧左端与小球M栓接,弹簧右端与固定挡板栓接。已知圆管的直径远小于轨道半径 且略大于小球直径,
且略大于小球直径, 和竖直方向之间的夹角
和竖直方向之间的夹角 ,
, 点与
点与 点的竖直高度差
点的竖直高度差 ,弹簧始终在弹性限度内,
,弹簧始终在弹性限度内, 。求:
。求:
(1)小球在 点抛出的水平初速度
点抛出的水平初速度
(2)小球运动到最低点 时,小球对轨道的压力
时,小球对轨道的压力 的大小(结果保留一位有效数字)
的大小(结果保留一位有效数字)
(3)弹簧压缩过程中,弹簧具有的最大弹性势能
(4)若只将弹簧右侧栓接的挡板改为栓接一个质量为 的光滑小球,水平轨道足够长,其它条件保持不变,则三个小球在整个运动和相互作用过程中小球
的光滑小球,水平轨道足够长,其它条件保持不变,则三个小球在整个运动和相互作用过程中小球 第二次达到最大速度时,小球M的速度是多少?
第二次达到最大速度时,小球M的速度是多少?