(本题10分)已知抛物线C: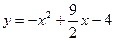 ,过原点O作抛物线C的切线
,过原点O作抛物线C的切线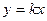 使切点P在第一象限,
使切点P在第一象限,
(1)求k的值;
(2)过点P作切线的垂线,求它与抛物线C的另一个交点Q的坐标。
某小组有6个同学,其中4个同学从来没有参加过数学研究性学习活动,2个同学曾经参加过数学研究性学习活动.
(I)现从该小组中任选2个同学参加数学研究性学习活动,求恰好选到1个曾经参加过数学研究性学习活动的同学的概率;
(II)若从该小组中任选2个同学参加数学研究性学习活动,活动结束后,该小组没有参加过数学研究性学习活动的同学个数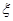 是一个随机变量,求随机变量
是一个随机变量,求随机变量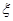 的分布列及数学期望
的分布列及数学期望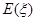 .
.
(选修4—4:坐标系与参数方程)
在极坐标系中,设圆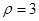 上的点到直线
上的点到直线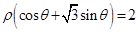 的距离为
的距离为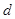 ,求
,求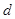 的最大值.
的最大值.
(选修4—2:矩阵与变换)
二阶矩阵M对应的变换将点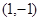 与
与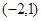 分别变换成点
分别变换成点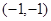 与
与 .
.
(Ⅰ)求矩阵M的逆矩阵 ;
;
(Ⅱ)设直线 在变换M作用下得到了直线
在变换M作用下得到了直线 :
: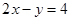 ,求直线
,求直线 的方程.
的方程.
已知数列 满足
满足 ,
, ,n∈N*.
,n∈N*.
(1)证明:数列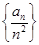 是等比数列,并求数列
是等比数列,并求数列 的通项公式;
的通项公式;
(2)设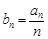 ,求
,求 ;
;
(3)设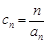 ,求证
,求证 <
<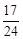 .
.
已知函数 在点
在点 处的切线方程为
处的切线方程为 .
.
⑴求函数 的解析式;
的解析式;
⑵若对于区间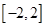 上任意两个自变量的值
上任意两个自变量的值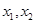 都有
都有 ,求实数
,求实数 的最小值;
的最小值;
⑶若过点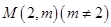 可作曲线
可作曲线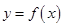 的三条切线,求实数
的三条切线,求实数 的取值范围.
的取值范围.