下表是某工厂10个车间2011年3月份产量的统计表，1到10车间的产量依次记为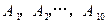
(如：
表示6号车间的产量为980件)．图2是统计下表中产量在一定范围内车间个数的一个算法流程图.那么算法流程(图2)输出的结果是( )
| 车间 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 产量 |
108 0 |
900 |
930 |
850 |
1500 |
980 |
960 |
900 |
830 |
1250 |
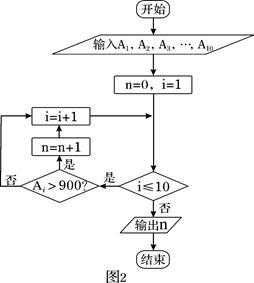
| A．5 | B．6 | C．4 | D．7 |
∈R，且
，则下列结论正确的是（ ）
B 
C 
D.
是等差数列，首项
，则使前n项和
成立的
（）
，a≠b且a＋b＝1，则
的取值范围是（ ）
的各项均为正数，公比
, 设
，
，则
与
的大小关系为（）
中，a=15,b=10,A=60°，则
="" ()
