(本题满分14分,第(1)小题满分4分,第(2)、(3)小题满分各5分)在Rt△ABC中,∠ACB=90°,BC=30,AB=50.点P是AB边上任意一点,直线PE⊥AB,与边AC或BC相交于E.点M在线段AP上,点N在线段BP上,EM=EN, .
.
(1)如图1,当点E与点C重合时,求CM的长;
(2)如图2,当点E在边AC上时,点E不与点A、C重合,设AP=x,BN=y,求y关于x的函数关系式,并写出函数的定义域;
(3)若△AME∽△ENB(△AME的顶点A、M 、E分别与△ENB的顶点E、N、B对应),求AP的
、E分别与△ENB的顶点E、N、B对应),求AP的 长.
长.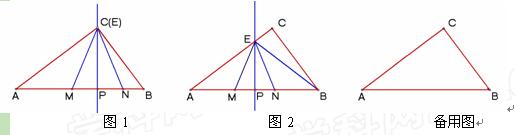
某农户种植一种经济作物,总用水量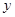 (
(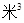 )与种植时间
)与种植时间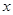 (天)之间的函数关系式如图所示.
(天)之间的函数关系式如图所示.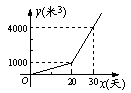
(1)求y与x之间的函数关系式.
(2)种植时间为多少天时,总用水量达到7000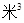 ?
?
解方程(每小题4分,共16分)
(1) (2)
(2)
(3) (4)
(4)
先化简,再求值: ,其中
,其中 .
.
分解因式(每小题3分,共6分)
(1)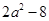 (2)
(2)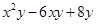
今年,号称“千湖之省”的湖北正遭受大旱,为提高学生环境意识,节约用水,某校数学教师编制了一道应用题:
为了保护水资源,某市制定一套节水的管理措施,其中对居民生活用水收费作如下规定:
| 月用水量(吨) |
单价(元/吨) |
| 不大于10吨部分 |
1.5 |
大于10吨不大于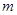 吨部分( 吨部分(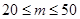 ) ) |
2 |
大于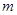 吨部分 吨部分 |
3 |
(1)若某用户六月份用水量为18吨,求其应缴纳的水费;
(2)记该用户六月份用水量为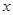 吨,缴纳水费为
吨,缴纳水费为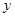 元,试列出
元,试列出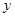 与
与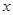 的函数式;
的函数式;
(3)若该用户六月份用水量为40吨,缴纳水费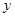 元的取值范围为
元的取值范围为 ,试求
,试求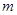 的取值范围。
的取值范围。