一内壁光滑的环形细圆管,位于竖直平面内,环的半径为R(比细管的内径大得多),在圆管中有两个直径略小于细管内径的小球(可视为质点)A、B,A球质量为m1,B球质量为m2,它们沿圆管顺时针运动,经过圆管最低点时速度都是v0,若某时刻A球在圆管最低点时,B球恰好在圆管最高点,两球作用于圆管的合力为零,求m1、m2、R与v0应满足的关系式。
飞机在竖直平面内做半径为400m的匀速圆周运动,其速度是150m/s,飞行员质量为80kg,g取10m/s2.求:
(1)飞机在轨道最低点飞行员头朝上时,飞行员对座椅的压力大小和方向。
(2)飞机在轨道最高点飞机员头朝下时,飞行员对座椅的压力大小和方向。
一个小球从离地面高度H=5m处的A点,以水平速度V0=6m/s水平抛出,不计空气阻力g取10m/s2。求:
(1)小球从抛出到落地所用的时间。
(2)小球从抛出起经0.8s时的速度大小和方向。
如图所示,在竖直平面内固定一半径R为2 m、圆心角为120°的光滑圆弧轨道BEC,其中点E是最低点.在B、C两端平滑、对称地连接长度S均为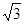 m的AB、CD两段粗糙直轨道,直轨道上端A、D与最低点E之间的高度差h均为2.5 m.现将质量为0.01 kg的小物块由A点静止释放,物块与直轨道间的动摩擦因数均为0.25.求:
m的AB、CD两段粗糙直轨道,直轨道上端A、D与最低点E之间的高度差h均为2.5 m.现将质量为0.01 kg的小物块由A点静止释放,物块与直轨道间的动摩擦因数均为0.25.求: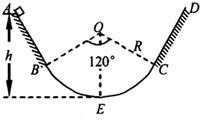
(1) 小物块从静止释放到第一次过E点时重力做的功;
(2) 小物块第一次通过E点时的动能大小;
(3) 小物块在E点时受到支持力的最小值.
如图所示,半径为R的圆轮在竖直面内绕O轴匀速转动,O轴离地面高为2R,轮上a、b两点与O点的连线相互垂直,a、b两点均粘有一小物体,当a点转至最低位置时,a.b两点处的小物体同时脱落,经过相同时间落到水平地面上。
(1)试判断圆轮的转动方向。
(2)求圆轮转动的角速度的大小。
宇航员在月球表面完成下面实验:如图所示,在一固定的竖直光滑圆弧轨道内侧最低点有一小球(可视为质点),当给小球一个水平方向的初速度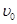 时,小球刚好能在竖直面内做完整的圆周运动.已知圆弧轨道半径为r,月球的半径为R,引力常量为G.
时,小球刚好能在竖直面内做完整的圆周运动.已知圆弧轨道半径为r,月球的半径为R,引力常量为G.
(1)若在月球表面发射一颗环月卫星,所需最小发射速度为多少?
(2)月球的平均密度为多大?