如图所示,一可视为质点的物体质量为m=1 kg,在左侧平台上水平抛出,恰能无碰撞地沿圆弧切线从A点进入光滑竖直圆弧轨道,并沿轨道下滑,A、B为圆弧两端点,其连线水平,O为轨道的最低点.已知圆弧半径为R=1.0 m,对应圆心角为θ=106°,平台与AB连线的高度差为h=0.8 m.(重力加速度g=10 m/s2,sin53°=0.8,cos53°=0.6)求:
(1)物体平抛的初速度;
(2)物体运动到圆弧轨道最低点O时对轨道的压力.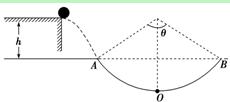
甲、乙两车从同一地点出发同向运动,其图象如图所示.试计算:
(1)从乙车开始运动多少时间后两车相遇?
(2)相遇处距出发多远?
(3)相遇前两车的最大距离是多少?
(8分一些同学乘坐动力组列车外出旅游,当火车在一段平直轨道上匀加速行驶时,一同学提议说:“我们能否用身边的器材测出火车的加速度?”许多同学参与了测量工作,测量过程如下:他们一边看着窗外每隔100 m的路标,一边用手表记录着时间,他们观测到从第一根路标运动到第二根路标的时间间隔为5 s,从第一根路标运动到第三根路标的时间间隔为9 s,请你根据他们的测量情况,求:(1)火车的加速度大小;
(2)他们到第三根路标时的速度大小。
一辆汽车从静止开始做匀加速直线运动,已知在2s内先后经过相距27m的A、B两点,汽车经过B点时的速度为15m/s。求:
(1)汽车经过A点的速度;
(2)汽车从出发点到A点的平均速度;
(3)A点与出发点间的距离
某物体的位移图象如图所示,若规定向东为正方向,试求物体在OA、CD、DE各阶段的速度大小及方向。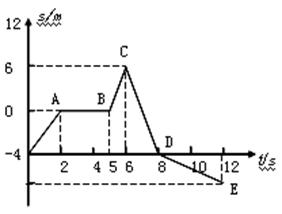
做匀加速运动的火车,在40s内速度从10m/s增加到20m/s,求火车加速度的大小.汽车紧急刹车时做匀减速运动,在2s内速度从10m/s减小到零,求汽车的加速度大小。