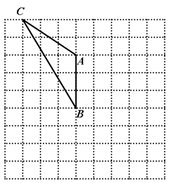
现有一张△ABC纸片,点D、E分别是△ABC边上两点,若沿直线DE折叠.如果折成图①的形状,使A点落在CE上,则∠1与∠A的数量关系是
如果折成图②的形状,猜想∠1+∠2和∠A的数量关系是
如果折成图③的形状,猜想∠1、∠2′和∠A的数量关系,并说明理由.
将问题1推广,如图④,将四边形ABCD纸片沿EF折叠,使点A、B落在四边形EFCD的内部时,∠1+∠2与∠A、∠B之间的数量关系是.

观察下列等式,并回答有关问题: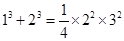 ;
;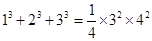 ;
;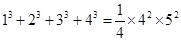 ;
;若n为正整数,猜想
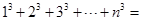 ;
;利用上题的结论比较
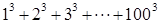 与
与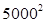 的大小.
的大小.
在△ABC中,AD是高,AE是角平分线.,∠B=20°,∠C=60,求∠CAD和∠DAE的度数.
如图,AB∥DC,∠ABC=∠ADC,问:AE与FC平行吗?请说明理由.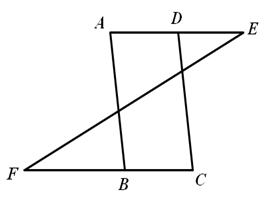
如图,△ABC的顶点都在方格纸的格点上,将△ABC向下平移3格,再向右平移4格.请在图中画出平移后的△A′B′C′
在图中画出△A′B′C′的高C′D′