甲、乙、两三个布袋都不透明,甲袋中装有1个红球和1个白球;乙袋中装有一个红球和2个白球;丙袋中装有2个白球.这些球除颜色外都相同.从这3个袋中各随机地取出1个球.
①取出的3个球恰好是2个红球和1个白球的概率是多少?
②取出的3个球全是白球的概率是多少?
如上图,在 正方形网格中,每个小正方形的边长均为1个单位.
正方形网格中,每个小正方形的边长均为1个单位.
(1)作 关于点P的对称图形
关于点P的对称图形 。
。
(2)再把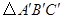 ,绕着
,绕着 逆顺时针旋转
逆顺时针旋转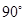 ,得到
,得到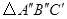 ,请你画出
,请你画出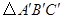 和
和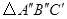 (不要求写画法).
(不要求写画法).
解方程:
计算: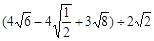
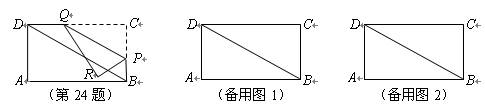
如图,在矩形 中,
中,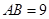 ,
,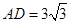 ,点
,点 是边
是边 上的动点(点
上的动点(点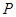 不与点
不与点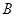 ,点
,点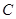 重合),过点
重合),过点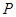 作直线
作直线 ,交
,交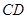 边于
边于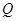 点,再把
点,再把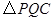 沿着动直线
沿着动直线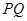 对折,点
对折,点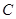 的对应点是
的对应点是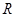 点,设
点,设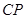 的长度为
的长度为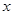 ,
,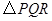 与矩形
与矩形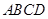 重叠部分的面积为
重叠部分的面积为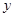 .
.
(1)求 的度数;
的度数;
(2)当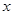 取何值时,点
取何值时,点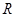 落在矩形
落在矩形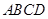 的
的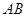 边上?
边上?
(3)①求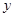 与
与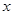 之间的函数关系式;
之间的函数关系式;
②当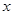 取何值时,重叠部分的面积等于矩形面积的
取何值时,重叠部分的面积等于矩形面积的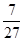 ?
?
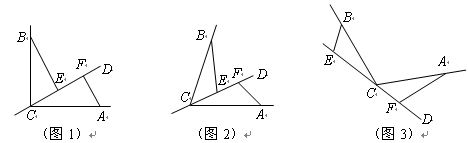
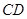 经过
经过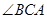 顶点
顶点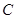 的一条直线,
的一条直线, .
.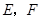 分别是直线
分别是直线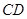 上两点,且
上两点,且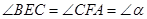 .
.
(1)若直线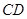 经过
经过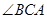 的内部,且
的内部,且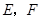 在射线
在射线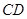 上,请解决下面两个问题:
上,请解决下面两个问题:
①如图1,若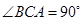 ,
,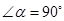 ,
,
则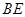
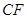 ;
;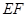
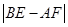 (填“
(填“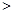 ”,“
”,“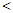 ”或“
”或“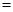 ”);
”);
②如图2,若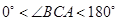 ,请添加一个关于
,请添加一个关于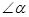 与
与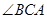 关系的条件,使①中的两个结论仍然成立,并证明两个结论成立.
关系的条件,使①中的两个结论仍然成立,并证明两个结论成立.
(2)如图3,若直线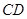 经过
经过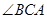 的外部,
的外部,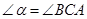 ,请提出
,请提出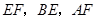 三条线段数量关系的合理猜想(不要求证明).
三条线段数量关系的合理猜想(不要求证明).