如图,梯形ABCD中,AD∥BC,BC=20cm,AD=10cm,现有两个动点P、Q
分别从B、D两点同时出发,点P以每秒2cm的速度沿BC向终点C移动,点Q以每秒1cm
的速度沿DA向终点A移动,线段PQ与BD相交于点E,过E作EF∥BC交CD于点F,射线
QF交BC的延长线于点H,设动点P、Q移动的时间为t(单位:秒,0<t<10).
(1)当t为何值时,四边形PCDQ为平行四边形?
(2)在P、Q移动的过程中,线段PH的长是否发生改变?如果不变,求出线段PH的长;如果改变,请说明理由.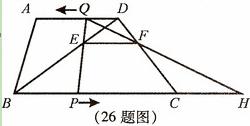
已知等边△ABC和Rt△DEF按如图所示的位置放置,点B,D重合,且点E、B(D)、C在同一条直线上.其中∠E=90°,∠EDF=30°,AB=DE=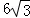 ,现将△DEF沿直线BC以每秒
,现将△DEF沿直线BC以每秒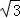 个单位向右平移,直至E点与C点重合时停止运动,设运动时间为t秒.
个单位向右平移,直至E点与C点重合时停止运动,设运动时间为t秒.
(1)试求出在平移过程中,点F落在△ABC的边上时的t值;
(2)试求出在平移过程中△ABC和Rt△DEF重叠部分的面积s与t的函数关系式;
(3)当D与C重合时,点H为直线DF上一动点,现将△DBH绕点D顺时针旋转60°得到△ACK,则是否存在点H使得△BHK的面积为 ?若存在,试求出CH的值;若不存在,请说明理由.
?若存在,试求出CH的值;若不存在,请说明理由.
正方形ABCD中,E为AD上的一点(不与A、D点重合),AD=nAE,BE的垂直平分线分别交AB、CD于F、G两点,垂足为H.
(1)如图1,当n=2时,则 = _________ ;
= _________ ;
(2)如图1,当n=2时,求 的值;
的值;
(3)延长FG交BC的延长线于M(如图2),直接填空:当n= _________ 时, .
.
如图,小明家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间的地板F处,中午太阳光恰好能从窗户的最低点D射进房间的地板E处,小明测得窗子距地面的高度OD=0.8m,窗高CD=1.2m,并测得OE=0.8m,OF=3m,求围墙AB的高度.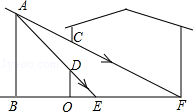
如图:公路旁有两个高度相等的路灯AB、CD.数学老师杨柳上午上学时发现路灯B在太阳光下的影子恰好落到里程碑E处,他自己的影子恰好落在路灯CD的底部C处.晚自习放学时,站在上午同一个地方,发现在路灯CD的灯光下自己的影子恰好落在里程碑E处.
(1)在图中画出杨老师的位置(用线段FG表示),并画出光线,标明(太阳光、灯光);
(2)若上午上学时候高1米的木棒的影子为2米,杨老师身高为1.5米,他离里程碑E恰5米,求路灯高.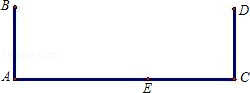
某数学兴趣小组开展了一次活动,过程如下:
设∠BAC=θ(0°<θ<90°).现把小棒依次摆放在两射线之间,并使小棒两端分别落在射线AB,AC上.
活动一:
如图甲所示,从点A1开始,依次向右摆放小棒,使小棒与小棒在端点处互相垂直,A1A2为第1根小棒.
数学思考:
(1)小棒能无限摆下去吗?答: _________ .(填“能”或“不能”)
(2)设AA1=A1A2=A2A3=1.
①θ= _________ 度;
②若记小棒A2n﹣1A2n的长度为an(n为正整数,如A1A2=a1,A3A4=a2,…)求出此时a2,a3的值,并直接写出an(用含n的式子表示).
活动二:
如图乙所示,从点A1开始,用等长的小棒依次向右摆放,其中A1A2为第1根小棒,且A1A2=AA1.
数学思考:
(3)若已经摆放了3根小棒,θ1= _________ ,θ2= _________ ,θ3= _________ ;(用含θ的式子表示)
(4)若只能摆放4根小棒,求θ的范围.