一枚棋子放在边长为1个单位长度的正六边形
ABCDEF的顶点A处，通过摸球来确定该棋子的走法，其规则是：在
一只不透明的袋子中，装有3个标号分别为1、2、3的相同小球，搅匀
后从中任意摸出1个，记下标号后放回袋中并搅匀，再从中任意摸出1
个，摸出的两个小球标号之和是几棋子就沿边按顺时针方向走几个单位
长度．
棋子走到哪一点的可能性最大？求出棋子走到该点的概率．（用列表或画树状图的方法
求解）
求证：在直角三角形中，如果有一个锐角等于30°，那么这个锐角所对的直角边等于斜边的一半
已知：等腰△ABC中，AB=AC=13，BC=10，求底角∠B的正弦、余弦、正切值。
如图，点E在AB上，点G在CD上，EF⊥GF于F，∠CGF=150°，∠BEF=60°，试判断AB和CD的位置关系，并说明理由.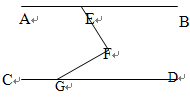
如图，点D、B分别在∠A的两边上，C是∠A内一点，且AB=AD，BC=DC，CE⊥AD，CF⊥AB，垂足分别为E、F求证：CE=CF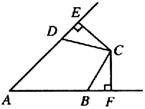
如果一个正整数能表示为两个连续偶数的平方差，那么称这个正整数为“神秘数”。如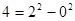
，
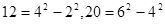. 因此,4、12、20这三个数都是神秘数
（1）、28和2012这两个数是神秘数吗？为什么？
（2）、设两个连续偶数为2k+2和2k（其中k取非负整数），由这两个连续偶数构造的神秘数是4的倍数吗？为什么？