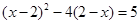某校开展了以“人生观、价值观”为主题的班队活动,活动结束后,初三(2)班数学兴趣小组提出了5个主要观点并在本班50名学生中进行了调查(要求每位同学只选自己最认可的一项观点),并制成了如下扇形统计图.
(1)该班学生选择“和谐”观点的有 人,在扇形统计图中,“和谐”观点所在扇形区域的圆心角是 度.
(2)如果该校有1500名初三学生,利用样本估计选择“感恩”观点的初三学生约有 人.
(3)如果数学兴趣小组在这5个主要观点中任选两项观点在全校学生中进行调查,求恰好选到“和谐”和“感恩”观点的概率(用树状图或列表法分析解答)
 |
(本题10分)
如图,在△ABC中,∠C=90º,BC=5米,AB=10米.M点在线段CA上,从C向A运动,速度为1米/秒;同时N点在线段AB上,从A向B运动,速度为2米/秒.运动时间为t秒.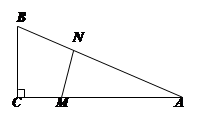
(1)当t为何值时,△AMN的面积为6米2?
(2)当t为何值时,△AMN的面积最大?并求出这个最大值.
阅读材料:如果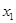 、
、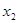 是一元二次方程
是一元二次方程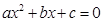 (
(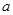 ≠0)的两根,那么,
≠0)的两根,那么,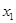 +
+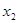 =
=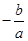 ,
,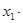
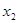 =
=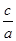 .这就是著名的韦达定理.
.这就是著名的韦达定理.
现在我们利用韦达定理解决问题:
已知 与
与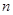 是方程
是方程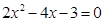 的两根,
的两根,
(1)填空: +
+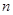 =________;
=________;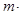
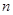 =________;
=________;
(2)计算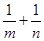 的值.
的值.
(本题8分)
在如图的4×4的方格内画△ABC,使它的顶点都在格点上,三条边长分别为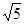 ,
,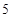 ,
, .
.
(本题8分)
已知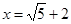 ,
,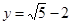 ,求下列各式的值:
,求下列各式的值:
(1)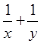 ;
;
(2)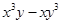 .
.
(每题4分,共16分)
解下列方程:
(1)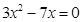
(2)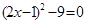
(3)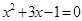
(4)