如图,飞机沿水平方向(A、B两点所在直线)飞行,前方有一座高山,为了避免飞机飞行过低,就必须测量山顶M到飞行路线AB的距离MN.飞机能够测量的数据有俯角和飞行的距离(因安全因素,飞机不能飞到山顶的正上方N处才测飞行距离),请设计一个距离MN的方案,要求:
(1)指出需要测量的数据(用字母表示,并在图中标出);
(2)用测出的数据写出求距离MN的步骤.
 |
如图所示,AB是⊙O的直径,AE是弦,C是劣弧AE的中点,过C作CD⊥AB于点D,CD交AE于点F,过C作CG∥AE交BA的延长线于点G.连接OC交AE于点H。
(1)求证:GC⊥OC.
(2)求证:AF=CF.
(3)若∠EAB=30°,CF=2,求GA的长.
已知函数y=mx2-6x+1(m是常数).
⑴求证:不论m为何值,该函数的图象都经过y轴上的一个定点;
⑵若该函数的图象与x轴只有一个交点,求m的值.
如图:在△ABC中,AB=2,BC=2 ,AC=4,点O是AC的中点;回答下列问题:
,AC=4,点O是AC的中点;回答下列问题:
(1)∠BAC=°
(2)画出将△ABC绕点O旋转180°得到的△A1DC1(A→A1B→D C→C1),写出四边形ABCD的形状。
(3)尺规作图:在图中作出△ABC的高线AE(保留作图痕迹),并回答在四边形ABCD的边上(点A除外)是否存在点F,使∠EAC=∠EFC; 若存在点F,写出这样的点F一共有几个?并直接写出DF的长。若不存在这样的点F,请简要说明理由。
已知关于x的方程 .
.
(1)若这个方程有实数根,求k的取值范围;
(2)若这个方程有一个根为1,求k的值;
(3)若以方程 的两个根为横坐标、纵坐标的点恰在反比例函数
的两个根为横坐标、纵坐标的点恰在反比例函数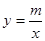 的图象上,求满足条件的m的最小值.
的图象上,求满足条件的m的最小值.
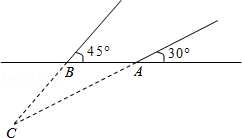
2013年3月,某煤矿发生瓦斯爆炸,该地救援队立即赶赴现场进行救援,救援队利用生命探测仪在地面A、B两个探测点探测到C处有生命迹象.已知A、B两点相距4米,探测线与地面的夹角分别是30°和45°,试确定生命所在点C的深度.(精确到0.1米,参考数据: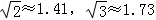 )
)