(本小题10分)设向量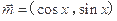 ,
, ,
,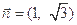 .
.
(Ⅰ)若 ,求
,求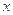 的值;
的值;
(Ⅱ)设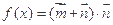 ,求函数
,求函数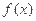 的值域.
的值域.
已知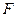 是椭圆
是椭圆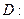
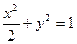 的右焦点,过点
的右焦点,过点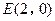 且斜率为
且斜率为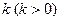 的直线
的直线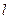 与
与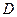 交于
交于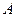 、
、 两点,
两点,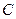 是点
是点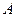 关于
关于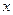 轴的对称点.
轴的对称点.
(Ⅰ)证明:点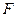 在直线
在直线
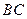 上;
上;
(Ⅱ)设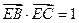 ,求
,求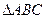 外接圆的方程.
外接圆的方程.
在一个有奖问答的电视节目中,参赛选手顺序回答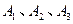 三个问题,答对各个问题所获奖金(单位:元)对应如下表:
三个问题,答对各个问题所获奖金(单位:元)对应如下表:
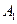 |
 |
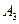 |
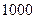 |
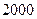 |
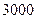 |
当一个问题回答正确后,选手可选择继续回答下一个问题,也可选择放弃.若选择放弃,选手将获得答对问题的累计奖金,答题结束;若有任何一个问题回答错误,则全部奖金归零,答题结束.设一名选手能正确回答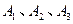 的概率分别为
的概率分别为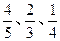 ,正确回答一个问题后,选择继续回答下一个问题的概率均为
,正确回答一个问题后,选择继续回答下一个问题的概率均为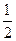 ,且各个
,且各个 问题回答正确与否互不影响.
问题回答正确与否互不影响.
(Ⅰ)按照答题规则,求该选手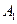 回答正确但所得奖金为零的概率;
回答正确但所得奖金为零的概率;
(Ⅱ)设该选手所获奖金总数为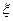 ,求
,求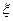 的分布列与数学期望.
的分布列与数学期望.
已知数列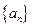 的前
的前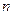 项和
项和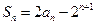 .
.
(Ⅰ)证明:数列 是等差数列;
是等差数列;
(Ⅱ)若不等式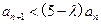 恒成立,求
恒成立,求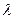 的取值范围.
的取值范围.
如图,正三棱柱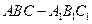 中,
中,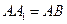 ,
,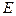 是侧棱
是侧棱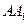 的中点.
的中点.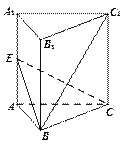
(Ⅰ)证明: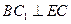 ;
;
(Ⅱ)求二面角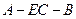 的大小.
的大小.
已知 的内角
的内角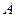 、
、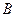 的对边分别为
的对边分别为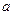 、
、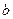 ,
,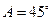 ,
,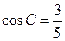 .
.
(Ⅰ)求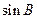 ;
;
(Ⅱ)若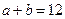 ,求
,求 的面积.
的面积.