图中滑块和小球的质量均为m,滑块可在水平放置的光滑固定导轨上自由滑动,小球与滑块上的悬点O由一不可伸长的轻绳相连,轻绳长为 .开始时,轻绳处于水平拉直状态,小球和滑块均静止.现将小球由静止释放,当小球到达最低点时,滑块刚好被一表面涂有粘住物质的固定挡板粘住,在极短的时间内速度减为零,小球继续向左摆动,当轻绳与竖直方向的夹角θ=60°时小球到达最高点.求
.开始时,轻绳处于水平拉直状态,小球和滑块均静止.现将小球由静止释放,当小球到达最低点时,滑块刚好被一表面涂有粘住物质的固定挡板粘住,在极短的时间内速度减为零,小球继续向左摆动,当轻绳与竖直方向的夹角θ=60°时小球到达最高点.求
(1)小球到达最低点时速度的大小;
(2)滑块与挡板刚接触的瞬时,滑块速度的大小;
(3)小球从释放到第一次到达最低点的过程中,绳的拉力对小球所做的功.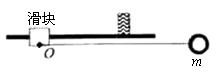
如图所示,物体从光滑斜面上的A点由静止开始下滑,经过B点后进入水平面(设经过B点前后速度大小不变),最后停在C点.每隔0.2秒钟通过速度传感器测量物体的瞬时速度,表给出了部分测量数据.(重力加速度g=10m/s2)
| t(s) |
0.0 |
0.2 |
0.4 |
… |
1.2 |
1.4 |
… |
| V(m/s) |
0.0 |
1.0 |
2.0 |
… |
1.1 |
0.7 |
… |

求:(1)物体在斜面上的加速度大小;
(2)物体与水平面之间的动摩擦因数μ;
(3)t=0.6s时的瞬时速度v.
汽车正以10m/s的速度在平直的公路上前进,突然发现正前方有一辆自行车以4m/s的速度做同方向的匀速直线运动,汽车立即关闭油门做加速度大小为6m/s2的匀减速运动,汽车恰好不碰上自行车,求关闭油门时汽车离自行车多远?
如图所示,离子发生器发射一束质量为m,电荷量为+q的离子,从静止经PQ两板间的加速电压加速后,以初速度v0再从a点沿ab方向进入一匀强电场区域,abcd所围成的正方形区域是该匀强电场的边界,已知正方形的边长为L,匀强电场的方向与ad边平行且由a指向d.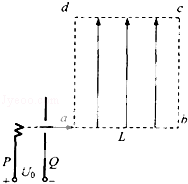
(1)求加速电压U0;
(2)若离子恰从c点飞离电场,求ac两点间的电势差Uac;
(3)若离子从边界上某点飞出时的动能为mv02,试判断离子从哪条边界飞出,并求此时匀强电场的场强大小E.
如图所示,电阻R1=8Ω,电动机绕组电阻R0=2Ω,当开关S断开时,电阻R1消耗的电功率是2.88W;当开关S闭合时,电阻R1消耗的电功率是2W.若电源的电动势为6V,求开关S闭合时
(1)干路中的总电流
(2)电动机输出的机械功率.
(3)若此电动机输出的机械功率不变,用它从静止开始竖直提升0.5Kg 物体时,物体匀速上升时的速度为多大.(g=10m/s2)
如图所示,匀强电场中A、B、C三点构成一个直角三角形中,∠A=30°,边长AC=32 cm.把电荷量q=﹣2×10﹣10C的点电荷由A点移到B点,电场力做功4.8×10﹣8J,再由B点移到C点,电荷克服电场力做功4.8×10﹣8J,取B点的电势为零,求
cm.把电荷量q=﹣2×10﹣10C的点电荷由A点移到B点,电场力做功4.8×10﹣8J,再由B点移到C点,电荷克服电场力做功4.8×10﹣8J,取B点的电势为零,求
(1)A、C两点的电势;
(2)匀强电场的场强.