如图所示，P是⊙O外一点，PA是⊙O的切线，A是切点，B是⊙O 上一点，且PA=PB，连接AO、BO、AB，并延长BO与切线PA相交于点Q．
（1）求证：PB是⊙O的切线；
（2）求证：AQ•PQ=OQ•BQ；
（3）设∠AOQ=α，若cosα=
，OQ=15，求AB的长．
如图，在边长为1个单位长度的小正方形组成的网格中，按要求画出△A1B1C1和△A2B2C2；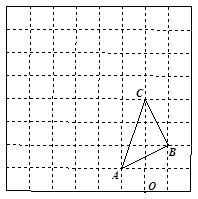
（1）将△ABC向左平移4个单位，得到△A1B1C1；
（2）以图中的O为位似中心，将△ABC作位似变换且放大到原来的两倍，得到△A2B2C2．
如图，在等边三角形ABC中，D、E分别在AC、AB上，且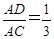
，
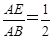．试说明：△ADE∽△CDB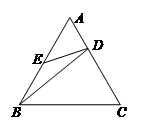
如图，在Rt△ABC中，∠C = 90°，∠A = 30°，AB = 4，求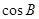
及AC．（结果保留根号）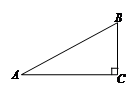
解方程：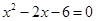
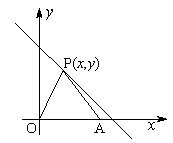
如图，在平面直角坐标系中，点P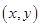
是第一象限直线
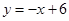上的点，点A
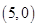，O是坐标原点，△PAO的面积为
.
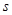⑴求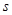与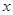
的函数关系式,并写出x的取值范围；
⑵探究：当P点运动到什么位置时△PAO的面积为10.