同学们，我们曾经研究过n×n的正方形网格，得到了网格中正方形的总数的表达式为
．但n为100时，应如何计算正方形的具体个数呢？下面我们就一起来探究并解决这个问题．首先，通过探究我们已经知道
时，我们可以这样做：
（1）观察并猜想：
=（1+0）×1+（1+1）×2=l+0×1+2+1×2=（1+2）+（0×1+1×2）
=（1+0）×1+（1+1）×
2+（l+2）×3
=1+0×1+2+1×2+3+
2×3
=（1+2+3）+（0×1+1×2+2×3）
=（1+0）×1+（1+1）×2+（l+2）×3+ ___________
="1+0×1+2+1×2+3+2×3+" ___________
=（1+2+3+4）+（___________）
…
（2）归纳结论：=（1+0）×1+（1+1）×2+（1+2）×3+…[1+（n-l）]n
=1+0×1+2+1×2+3+2×3+…+n+（n-1）×n
=（___________）+[ ___________]
=" ___________+" ___________
=
×___________
（3 ）实践应用：
通过以上探究过程，我们就可以算出当n为100时，正方形网格中正方形的总个数是_________。
小江玩投掷飞镖的游戏,他设计了一个如图所示的靶子,点E,F分别是矩形ABCD的两边AD,BC上的点,且EF∥AB,点M,N是EF上任意两点,则投掷一次,飞镖落在阴影部分的概率是。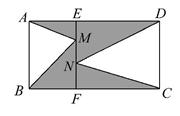
如图，矩形OABC的顶点A、C分别在x、y轴的正半轴上，点D为对角线OB的中点，点E（4，n）在边AB上，反比例函数
（k≠0）在第一象限内的图象经过点D、E，且D点的横坐标是它的纵坐标的2倍．
（1）求边AB的长；
（2）求反比例函数的解析式和n的值；
（3）若反比例函数的图象与矩形的边BC交于点F，将矩形折叠，使点O与点F重合，折痕分别与x、y轴正半轴交于点H、G，求线段OG的长．
已知反比例函数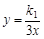
的图象与一次函数
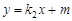的图象交于A（﹣1，a）、B（
，﹣3）两点，连结AO．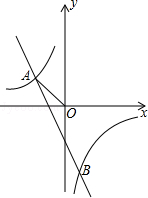
（1）求反比例函数和一次函数的表达式；
（2）设点C在y轴上，且与点A、O构成等腰三角形,求点C的坐标．
（本题满分
分）如图，在△ABC中，∠ABC=90°，D是边AC上的一点，连接BD，使∠A=2∠1，E是BC上的一点，以BE为直径的⊙O经过点D．
（1）求证：AC是⊙O的切线；
（2）若∠A=60°，⊙O的半径为2，求阴影部分的面积．（结果保留根号和π）
（本题满分
分）某商场出售一批进价为2元的贺卡，在市场营销中发现此商品的日销售单价x元与日销售量y之间有如下关系：
| X（元） |
3 |
4 |
5 |
6 |
| y（个） |
20 |
15 |
12 |
10 |
（1）根据表中的数据在平面直角坐标系中描出实数对（x,y）的对应点．
（2）猜测并确定y与x之间的函数关系式，并画出图象；
（3）设经营此贺卡的销售利润为w元，试求出w与x之间的函数关系式，若物价局规定此贺卡的销售价最高不能超过10元／个，请你求出当日销售单价x定为多少元时，才能获得最大日销售利润？