圆x2+y2-2x-1=0关于直线2x-y+3=0对称的圆的方程是( )
A.(x+3)2+(y-2)2=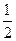 |
B.(x+3)2+(y+2)2=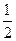 |
| C.(x+3)2+(y-2)2="2" | D.(x+3)2+(y+2)2=2 |
在空间四边形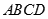 各边
各边 上分别取
上分别取 四点,如果与
四点,如果与 能相交于点
能相交于点 ,那么()
,那么()
A.点必 在直线BD上 在直线BD上 |
B.点 必在直线 必在直线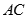 上 上 |
C.点 必在平面 必在平面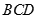 内 内 |
D.点 必在平面 必在平面 外 外 |
下列说法正确的是()
A.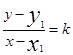 表示过点P(x1,y1)的所有直线方程. 表示过点P(x1,y1)的所有直线方程. |
| B.直线y=kx+b与y轴交于一点B(0,b),其中截距b=|OB|. |
C.在x轴和y轴上的截距分别为a与b的直线方程是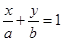 . . |
| D.方程(x2-x1)(y-y1)=(y2-y1)(x-x1) 表示过任意两点P1(x1,y1),P2(x2,y2)的直线 |
已知集合 ,N=
,N= ,若
,若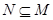 ,则
,则 的值是()
的值是()
A.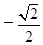 |
B.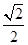 |
C. |
D.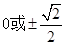 |
以每束1.6元价格处理.根据前五年销售情况预测,节日期间这种鲜花的需求量X服从如下表所示的分布:
 |
200 |
300 |
400 |
500 |
 |
0.20 |
0.35 |
0.30 |
0.15 |
若进这种鲜花500束,则利润的均值为()
A.706元 B.690元 C.754元 D.720元
设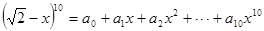 ,则
,则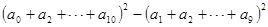 的值为()
的值为()
| A.0 | B.-1 | C.1 | D. |