(本小题满分12分)某工厂家具车间造A,B型两类桌子,每张桌子需木工和漆工两道工序完成.已知木工做一张A,B型桌子分别需要1 h和2 h,漆工油漆一张A,B型桌子分别需要3 h和1 h;又知木工、漆工每天工作分别不得超过8 h和9 h,而工厂造一张A,B型桌子分别获利润2千元和3千元,试问:工厂每天应生产A,B型桌子各多少张,才能获得最大利润?
已知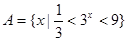 ,
,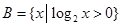 .
.
(1)求 和
和 ;
;
(2)定义 且
且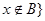 ,求
,求 和
和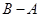 .
.
已知函数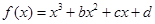 在区间
在区间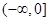 和
和 上单调递增,在
上单调递增,在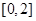 上单调递减,其图象与
上单调递减,其图象与 轴交于
轴交于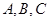 三点,其中点
三点,其中点 的坐标为
的坐标为 .
.
(1)求 的值;
的值;
(2)求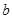 的取值范围;
的取值范围;
(3)求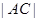 的取值范围.
的取值范围.
知椭圆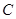 的两焦点
的两焦点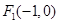 、
、 ,离心率为
,离心率为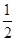 ,直线
,直线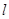 :
: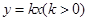 与椭圆
与椭圆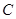 交于
交于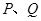 两点,点
两点,点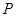 在
在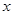 轴上的射影为点
轴上的射影为点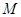 .
.
(1)求椭圆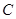 的标准方程;
的标准方程;
(2)求直线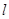 的方程,使
的方程,使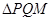 的面积最大,并求出这个最大值.
的面积最大,并求出这个最大值.
某校要建一个面积为450平方米的矩形球场,要求球场的一面利用旧墙,其他各面用钢筋网围成,且在矩形一边的钢筋网的正中间要留一个3米的进出口(如图).设矩形的长为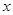 米,钢筋网的总长度为
米,钢筋网的总长度为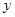 米.
米.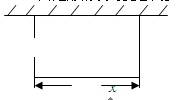
(1)列出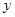 与
与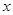 的函数关系式,并写出其定义域;
的函数关系式,并写出其定义域;
(2)问矩形的长与宽各为多少米时,所用的钢筋网的总长度最小?
(3)若由于地形限制,该球场的长和宽都不能超过25米,问矩形的长与宽各为多少米时,所用的钢筋网的总长度最小?
设曲线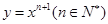 在点
在点 处的切线与
处的切线与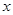 轴的交点坐标为
轴的交点坐标为 .
.
(1)求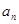 的表达式;
的表达式;
(2)设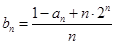 ,求数列
,求数列 的前
的前 项和
项和