（11·湖州）（本小题8分）
如图，已知AB是⊙O的直径，弦CD⊥AB，垂足为E，∠AOC=60°，OC=2。
⑴求OE和CD的长；
⑵求图中阴影部队的面积。
如图，点M是线段AB的中点，N在MB上，MN=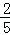
AM，若AM=15cm．求线段NB的长．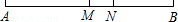
如图，直线AB，CD相交于点O，∠AOC=60°，∠1：∠2=1：2．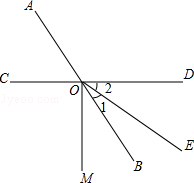
（1）求∠2的度数；
（2）若∠2与∠MOE互余，求∠MOB的度数．
为响应“让阅读走进生活”的号召，某中学七年级（1）班的老师为本班学生准备了若干本课外阅读书籍分发给大家，若每人3本还剩10本，若每人4本，则差36本，求本班有多少人，多少本书？
当m为何值时，关于x的方程4x+2m=3x﹣5的解和方程6x﹣8=10的解相同？
读语句画图，再填空，如图：
（1）画直线AB，线段AC，射线BC；
（2）取线段AC的中点D，连接BD；
（3）图中以B为端点的线段有 条．