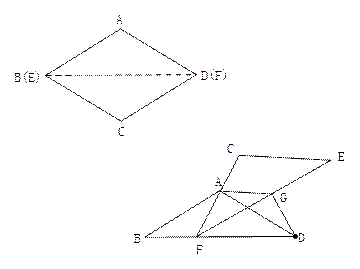
如图①，将菱形纸片AB（E）CD（F）沿对角线BD（EF）剪开，得到△ABD和△ECF，固定△ABD，并把△ABD与△ECF叠放在一起
（1）操作：如图②，将△ECF的顶点F固定在△ABD的BD边上的中点处，将△ECF绕点F在BD的上方左右旋转，设旋转时FC交BA于H（不与点B重合），EF交DA于G（不与点D重合），求证：BH·GD=BF2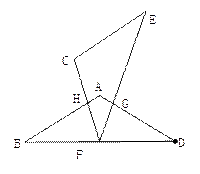
（2）操作：如图③，△ECF的顶点F在△ABD的BD边上滑动（不与点B、D重合），且CF如终过点A，过点A作AG∥CE，交EF于G，连接DG
探究：FD+DG= ，并请证明你的结论
 |
如图，用火柴棒按以下方式搭小鱼，是课本上多次出现的数学活动．
（1）搭n条小鱼需要火柴棒________根；
（2）计算说明150根火柴棒最多可以搭出多少条小鱼？
（3）若搭n朵某种小花需要火柴棒（3n+20）根，现有一堆火柴棒，可以全部用上搭出m条小鱼，也可以全部用上搭出m朵小花，求m的值及这堆火柴棒的数量．
从2开始，连续的偶数相加，它们和的情况如下表：
| 加数n的个数 |
和S |
| 1 |
2=1×2 |
| 2 |
2+4=6=2×3 |
| 3 |
2+4+6=12=3×4 |
| 4 |
2+4+6+8=20=4×5 |
| 5 |
2+4+6+8+10=30=5×6 |
| … |
… |
当n个最小的连续偶数（从2开始）相加时，它们的和与n之间有什么样的关系，请用公式表示出来，并由此计算：
①2+4+6+…+202的值；
②126+128+130+…+300的值．
国庆长假里，小华和爸爸、妈妈一家三口去旅游，甲旅行社说：“大人买全票，小孩半价优惠”．乙旅行社说：“大人、小孩全部按票价的八折优惠”．若原票价为α元，问小华家选择哪个旅行社合算，请说出理由．
用代数式表示阴影部分的面积．
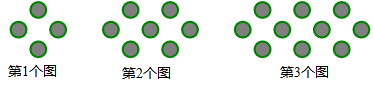
观察图中的棋子：
（1）按照这样的规律摆下去，第4个图形中的棋子个数是多少？
（2）用含n的代数式表示第n个图形的棋子个数；
（3）求第20个图形需棋子多少个？