某工厂有一种材料,可加工甲、乙、丙三种型号机械配件共240件,厂方计划由20个工人一天内加工完成,并要求每人只加工一种配件,根据下表提供的信息,解答下列问题:
| 配件种类 |
甲 |
乙 |
丙 |
| 每人可加工配件的数量(个) |
16 |
12 |
10 |
| 每个配件获利(元) |
6 |
8 |
5 |
(1)设加工甲种配件的人数为x,加工乙种配件的人数为y,求y与x之间的函数关系式
(2)如果加工每种配件的人数均不少于3人,那么加工配件的人数安排方案有几种?并写出每种安排方案
(3)要使此次加工配件的利润最大,应采用哪种方案?最大利润是多少?
2009年4月7日,国务院公布了《医药卫生体制改革近期重点实施方案(2009~2011年》,某市政府决定2009年投入6000万元用于改善医疗卫生服务,比2008年增加了1250万元.投入资金的服务对象包括“需方”(患者等)和“供方”(医疗卫生机构等),预计2009年投入“需方”的资金将比2008年提高30%,投入“供方”的资金将比2008年提高20%.
(1).该市政府2008年投入改善医疗卫生服务的资金是多少万元?
(2).该市政府2009年投入“需方”和“供方”的资金各多少万元?
(3).该市政府预计2011年将有7260万元投入改善医疗卫生服务,若从2009~2011年每年的资金投入按相同的增长率递增,求2009~2011年的年平均增长率.
已知:如图,在平面直角坐标系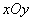 中,直线AB分别与
中,直线AB分别与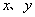 轴交于点B、A,与反比例函数的图象分别交于点C、D,
轴交于点B、A,与反比例函数的图象分别交于点C、D,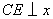 轴于点E,
轴于点E, .
.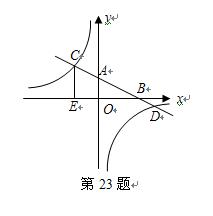
(1).求该反比例函数的解析式;
(2).求直线AB的解析式
省教委在推进课堂教学改革的过程中,为了切实减轻学生的课业负担,对义务教育阶段低年级学生原则上要求老师不布置课外作业,九年级学生每天的课外作业总时间不得超过1小时(学生阅读、自学除外):为了了解各校情况,县教委对其中40个学校九年级学生课外完成作业时间调研后进行了统计,并根据收集的数据绘制了下面两幅不完整的统计图,请你根据图中提供的信息,解答下面的问题:
(1).计算出学生课外完成作业时间在30~45分钟的学校对应的扇形圆心角;
(2).将图中的条形图补充完整;
(3).计算出学生课外完成作业时间在60~75分钟的学校占调研学校总数的百分比.
如图,⊙O的直径AB=4,C为圆周上一点,AC=2,过点C作⊙O的切线l,过点B作l的垂线BD,垂足为D,BD与⊙O交于点 E. 
(1).求∠AEC的度数;
(2).求证:四边形OBEC是菱形.
解不等式组: ,并将其解集在数轴上表示出来.
,并将其解集在数轴上表示出来. 