已知:如图,BD为⊙O的直径,AB=AC,AD交BC与E,AE=2,ED=4.
(1)求证:△ABE∽△ADB;
(2)求AB的长;
(3)延长DB到F,使BF=OB,连接FA,试判断直线FA与⊙O的位置关系,并说明理由.
如图,∠1=100°,∠2=100°,∠3=120°,填空: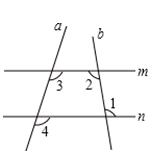
∵∠1=∠2=100°(已知)
∴ _______ ∥ _______ (内错角相等,两直线平行)
∴∠ ______ =∠ _____ (两直线平行,同位角相等)
又∵∠3=120°(已知)
∴∠4= _____ 度.
如图①所示,已知 、
、 为直线
为直线 上两点,点
上两点,点 为直线
为直线 上方一动点,连接
上方一动点,连接 、
、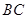 ,分别以
,分别以 、
、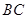 为边向
为边向 外作正方形
外作正方形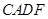 和正方形
和正方形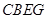 ,过点
,过点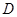 作
作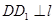 于点
于点 ,过点
,过点 作
作 于点
于点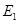 .
.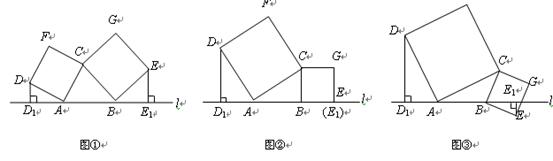
(1)如图②,当点 恰好在直线
恰好在直线 上时(此时
上时(此时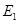 与
与 重合),试说明
重合),试说明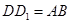 ;
;
(2)在图①中,当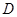 、
、 两点都在直线
两点都在直线 的上方时,试探求三条线段
的上方时,试探求三条线段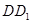 、
、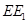 、
、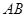 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
(3)如图③,当点 在直线
在直线 的下方时,请直接写出三条线段
的下方时,请直接写出三条线段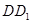 、
、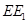 、
、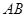 之间的数量关系.(不需要证明)
之间的数量关系.(不需要证明)
(1) 如图1,在正方形ABCD中,点E,F分别在边BC,CD上,AE,BF交于点O,∠AOF=90°.求证:BE=CF.
(2) 如图2,在正方形ABCD中,点E,H,F,G分别在边AB,BC,CD,DA上,EF,GH交于点O,∠FOH=90°, EF=4.求GH的长.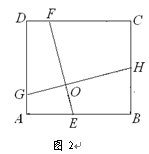
(3) 已知点E,H,F,G分别在矩形ABCD的边AB,BC,CD,DA上,EF,GH交于点O,∠FOH=90°,EF=4. 直接写出下列两题的答案:
①如图3,矩形ABCD由2个全等的正方形组成,求GH的长;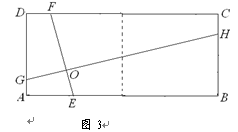
②如图4,矩形ABCD由n个全等的正方形组成,求GH的长(用n的代数式表示).
如图,在四边形ABCD中,∠BAC=∠ACD=90°,∠B=∠D.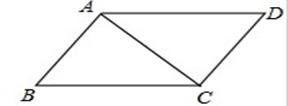
(1)求证:四边形ABCD是平行四边形;
(2)若AB=3cm,BC=5cm,点P从B点出发,以1cm/s的速度沿BC→CD→DA运动至A点停止,则从运动开始经过多少时间,△ABP为等腰三角形?
如图,已知E、F分别是▱ABCD的边BC、AD上的点,且BE=DF.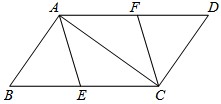
(1)求证:四边形AECF是平行四边形;
(2)若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长.