已知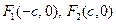 是椭圆
是椭圆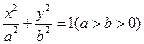 的左、右焦点,过点
的左、右焦点,过点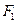 作
作
倾斜角为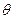 的动直线
的动直线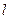 交椭圆于
交椭圆于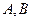 两点.当
两点.当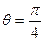 时,
时,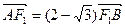 ,且
,且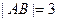 .
.
(1)求椭圆的离心率及椭圆的标准方程;
(2)求△ 面积的最大值,并求出使面积达到最大值时直线
面积的最大值,并求出使面积达到最大值时直线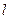 的方程
的方程 .
.
已知函数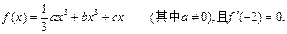
(1)若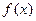 在x=2处取得极小值-2,求
在x=2处取得极小值-2,求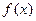 的单调区间;
的单调区间;
(2)令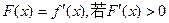 的解集是A,且A∪(0,1)=(-∞,1),求
的解集是A,且A∪(0,1)=(-∞,1),求 的最大值.
的最大值.
已知数列 中,a1=1,a2=3,且
中,a1=1,a2=3,且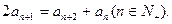 数列
数列 的前n项和为Sn,其中
的前n项和为Sn,其中
(1)求数列 和
和 的通项公式;
的通项公式;
(2)若 的表达式.
的表达式.
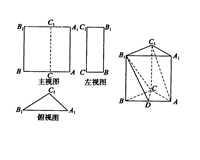
已知三棱柱ABC—A1B1C1的三视图如图所示,其中主视图AA1B1B和左视图B1BCC1均为矩形,俯高图△A1B1C1中,A1C1=3,A1B1=5,
(1)在三棱柱ABC—A1B1C1中,求证:BC⊥AC1;
(2)在三棱柱ABC—A1B1C1中,若D是底边AB的中点,求证:AC1∥平面CDB1;
(3)若三棱柱的高为5,求三视图中左视图的面积.
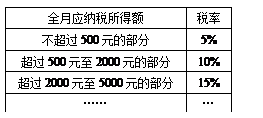
《中华人民共和国个人所得税法》规定,公民全月工资、薪金所得不超过起征点的部分不必纳税,超过起征点的部分为全月应纳税所得额,此项税款按下表分段累进计算:
第十届全国人大常委会第三十一次会议决定,个人所得税起征点自2008年3月1日起由1 600元提高到2 000元.
(1)某公民A全月工资、薪金所得额为3 250,请计算由于个人所得税起征点的调整,该公民A今年三月份的实际收入比二月份多了多少元?
(2)某公民B由于个人所得税起征点的调整,今年三月份的实际收入比二月份多了35元,计算该公民B三月份工资、薪金所得额为多少元?
已知向量: ,
,
函数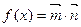 ,若
,若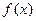 相邻两对称轴间的距离为
相邻两对称轴间的距离为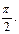
(1)求 的值,并求
的值,并求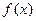 的最大值及相应x的集合;
的最大值及相应x的集合;
(2)在△ABC中,a,b,c分别是A,B,C所对的边,△ABC的面积 ,求边a的长.
,求边a的长.