(本小题满分12分)某区组织群众性登山健身活动,招募了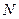 名师生志愿者,将所有志愿者现按年龄情况分为
名师生志愿者,将所有志愿者现按年龄情况分为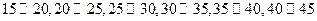 等六个层次,其频率分布直方图如图所示: 已知
等六个层次,其频率分布直方图如图所示: 已知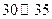 之间的志愿者共
之间的志愿者共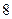 人.
人.
(Ⅰ)求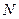 和
和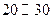 之间的志愿者人数
之间的志愿者人数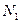 ;
;
(Ⅱ)已知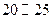 和
和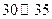 之间各有
之间各有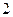 名英语教师,现从这两个层次各选取
名英语教师,现从这两个层次各选取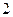 人担任接待工作,设两组的选择互不影响,求两组选出的人选中都至少有1名英语教师的概率是多少?
人担任接待工作,设两组的选择互不影响,求两组选出的人选中都至少有1名英语教师的概率是多少?
(Ⅲ)组织者从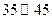 之间的志愿者(其中共有
之间的志愿者(其中共有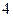 名女教师,其余全为男教师)中随机选取
名女教师,其余全为男教师)中随机选取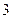 名担任后勤保障工作,其中女教师的数量为
名担任后勤保障工作,其中女教师的数量为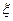 ,求
,求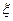 的概率和分布列.
的概率和分布列.
(本小题满分12分)已知函数
(1)求 取得最大值时,
取得最大值时,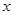 取值的集合与
取值的集合与 最大值
最大值
(2)若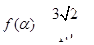 ,求
,求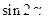 的值.
的值.
(本小题满分14分)如图所示,椭圆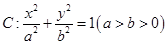 的左右焦点分别为
的左右焦点分别为 ,点
,点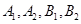 为椭圆
为椭圆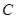 与坐标轴的交点,其中
与坐标轴的交点,其中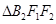 为等边三角形且面积为
为等边三角形且面积为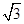 .
.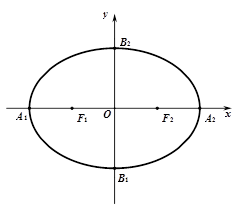
(1)求椭圆C的标准方程;
(2)过椭圆C的右顶点A2作两条互相垂直的直线分别和椭圆交于另一点P,Q,试判断直线PQ是否过定点,若过定点,求出该定点的坐标;若不过定点,请说明理由.
(本小题满分14分)设正数数列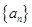 的前n项和为
的前n项和为 ,且满足
,且满足 (
( )
)
(1)求证: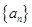 是等差数列;
是等差数列;
(2)设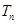 为数列{
为数列{ }的前n项和,求
}的前n项和,求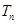 ;
;
(3)设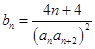 ,证明:
,证明: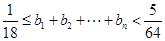 .
.
(本小题满分14分) 如图所示,平面
 平面
平面 ,且四边形
,且四边形 为
为
正方形,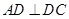 ,
, ∥
∥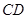 ,
, ,
, 为
为 的中点.
的中点.
(1)求证: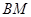 ∥平面
∥平面 ;
;
(2)求证: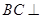 平面
平面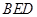 ;
;
(3)求平面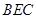 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.
(本小题满分12分)广东某高中进行高中生歌唱比赛,在所有参赛成绩中随机抽取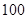 名学生的成绩,按成绩分组:第
名学生的成绩,按成绩分组:第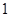 组
组 ,第
,第 组
组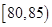 ,第
,第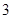 组
组 ,第
,第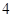 组
组 ,第
,第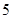 组
组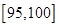 得到的频率分布直方图如图所示.现在组委会决定在笔试成绩高的第
得到的频率分布直方图如图所示.现在组委会决定在笔试成绩高的第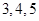 组中用分层抽样抽取
组中用分层抽样抽取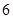 名学生进入第二轮面试.
名学生进入第二轮面试.
(1)求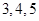 组各应该抽取多少人进入第二轮面试;
组各应该抽取多少人进入第二轮面试;
(2)学校决定在(1)中抽取的这6名学生中随机抽取2名学生接受考官D的面试,设第4组中有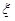 名学生被考官D面试,求
名学生被考官D面试,求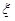 的分布列和数学期望.
的分布列和数学期望.