（本小题满分12分）已知椭圆
的中心在原点，焦点在
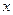轴上，点
分别是椭圆的左、右焦点，在直线
(
分别为椭圆的长半轴和半焦距的长)上的点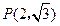
，满足线段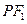
的中垂线过点
．过原点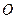
且斜率均存在的直线
、
互相垂直，且截椭圆所得的弦长分别为
、
．
(Ⅰ)求椭圆的方程；
(Ⅱ)求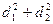
的最小值及取得最小值时直线、的方程.
本小题满分14分）若不等式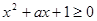
对
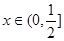恒成立，求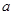
的最小值.
.如图，四棱锥S-ABCD的底面是正方形，每条侧棱的长都是地面边长的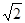
倍，P为侧棱SD上的点。
（1）求证：AC⊥SD；
（2）若SD⊥平面PAC，求二面角P-AC-
D的大小
（3）在（2）的条件下，侧棱SC上是否存在一点E，使得BE∥平面PAC。若存在，求SE：EC的值；若不存在，试说明理由。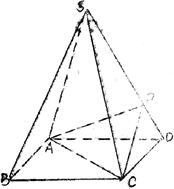
.如图，正方形ABCD所在平面与平面四边形ABEF所在平面互相垂直，△A
BE是等腰直角三角形，AB=AE，FA=FE，∠AEF=40°
（1）求证：EF⊥平面BCE；
（2）设线段CD、AE的中点分别为P、M，求证：PM∥平面BCE
（3）求二面角F—BD—A的大小。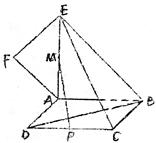
在四棱锥P－ABCD中，底面ABCD是矩形
，PA⊥平面ABCD，PA=AD=A，AB=2，以AC的中点O为球心、AC为直径的球面交PD于点M。
（1）求证：平面ABM⊥平面PCD；
（2）求直线CD与平面ACM所成的角的大小；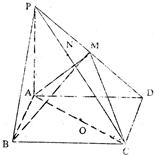
已知△ABC的面积S满足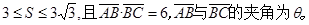
（Ⅰ）求θ的取值范围；
（Ⅱ）求函数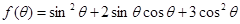
的最大值。