(8分)小华是某校八年级一班的学生,他班上最高的男生大伟的身高是174cm,
最矮的男生小刚的身高是150cm,为了参加学校篮球队的选拔,小华对班上30名男生的身
高(单位:cm)进行了统计.
请你根据上面不完整的频率分布表,解答下列问题:
(1)表中a和b所表示的数分别为a= ,b= ;
(2)小华班上男生身高的极差是 cm;
(3)身高的中位数落在哪个分组? ;
(4)若身高不低于165cm的男生可以参加选拔,则符合条件的男生占全班男生的百分之几?
在一个不透明的口袋中装有白、黄两种颜色的乒乓球(除颜色外其余都相同),其中黄球有1个,白球有2个. 第一次摸出一个球,做好记录后放回袋中,第二次再摸出一个球,请用列表或画树状图的方法求两次都摸到黄球的概率.
第一次摸出一个球,做好记录后放回袋中,第二次再摸出一个球,请用列表或画树状图的方法求两次都摸到黄球的概率.
已知:如图,将正方形ABCD纸片折叠,使顶点A落在边CD上的点P处(点P与C、D不重合),点B落在点Q处,折痕为EF,PQ与BC交于点G.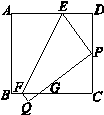
求证:△PCG∽△EDP.
已知:如图,AB是⊙O的弦,半径OC、OD分别交AB于点E、F,且AE="BF."
求证:OE=O F
F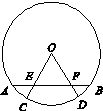
已知二次函数 .
.
(1)在给定的直角坐标系中,画出这个函数图象的示意图;
(2)根据图象,写出当
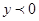 时
时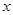 的取值范围.
的取值范围.
已知:如图,在Rt△ABC中,
 的正弦、余弦值.
的正弦、余弦值.