如图所示,某透明液体深1m,一束与水平面成300角的光线从空气射向该液体,进入该液体的光线与水平面的夹角为450。试求:
(1)该液体的折射率;
(2)进入液体的光线经多长时间可以照到底面。
在游乐场,有一种大型游乐设施跳楼机,如图所示,参加游戏的游客被安全带固定在座椅上,提升到离地最大高度64m处,然后由静止释放,开始下落过程可认为自由落体运动,然后受到一恒定阻力而做匀减速运动,且下落到离地面4m高处速度恰好减为零。已知游客和座椅总质量为1500kg,下落过程中最大速度为20m/s,重力加速度g=10m/s2。求:
(1)游客下落过程的总时间;(2)恒定阻力的大小。
(9分)某些建筑材料可产生放射性气体——氡,氡可以发生α或β衰变,如果人长期生活在氡浓度过高的环境中,那么,氡经过人的呼吸道沉积在肺部,并放出大量的射线,从而危害人体健康。原来静止的氡核( Rn)发生一次α衰变生成新核钋(Po),并放出一个能量为E0=0.09 MeV的光子。已知放出的α粒子动能为Eα=5.55 MeV;忽略放出光子的动量,但考虑其能量;1 u =931.5 MeV/ c2 。
Rn)发生一次α衰变生成新核钋(Po),并放出一个能量为E0=0.09 MeV的光子。已知放出的α粒子动能为Eα=5.55 MeV;忽略放出光子的动量,但考虑其能量;1 u =931.5 MeV/ c2 。
①写出衰变的核反应方程;
②衰变过程中总的质量亏损为多少?(保留三位有效数字)。
有一顶角为直角的玻璃砖,放在空气中,一光束斜射入玻璃砖的一个侧面,如图所示,然后投射到它的另一个侧面。若该玻璃砖全反射临界角为42°,问:
①这束光线能否从另一侧面射出?
②若光线能从侧面射出,玻璃砖折射率应满足何条件?
如图所示,“13”形状的各处连通且粗细相同的细玻璃管竖直放置在水平地面上,只有竖直玻璃管FG中的顶端G开口,并与大气相通,水银面刚好与顶端G平齐。AB =" CD" = L,BD =" DE" =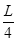 ,FG =
,FG =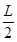 。管内用水银封闭有两部分理想气体,气体1长度为L,气体2长度为L/2,L = 76cm。已知大气压强P0 = 76cmHg,环境温度始终为t0 = 27℃,现在仅对气体1缓慢加热,直到使BD管中的水银恰好降到D点,求此时(计算结果保留三位有效数字)
。管内用水银封闭有两部分理想气体,气体1长度为L,气体2长度为L/2,L = 76cm。已知大气压强P0 = 76cmHg,环境温度始终为t0 = 27℃,现在仅对气体1缓慢加热,直到使BD管中的水银恰好降到D点,求此时(计算结果保留三位有效数字)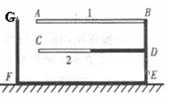
① 气体2的压强P2为多少厘米汞柱?
② 气体1的温度需加热到多少摄氏度?
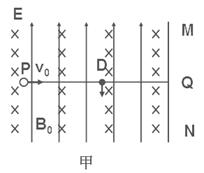
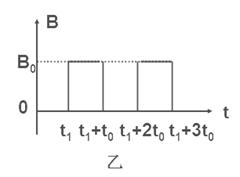
如图甲所示,竖直面MN的左侧空间存在竖直向上的匀强电场(上、下及左侧无边界)。一个质量为m、电量为q的可视为质点的带正电的小球,以大小为v0的速度垂直于竖直面MN向右作直线运动。小球在t=0时刻通过电场中的P点,为使小球能在以后的运动中竖直向下通过D点(P、D间距为L,且它们的连线垂直于竖直平面MN,D到竖直面MN的距离DQ等于L/π),经过研究,可以在电场所在的空间叠加如图乙所示随时间周期性变化的、垂直纸面向里的磁场,设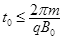 且为未知量。求:
且为未知量。求:
(1)场强E的大小;
(2)如果磁感应强度B0为已知量,试推出满足条件t1的表达式;
(3)进一步的研究表明,竖直向下的通过D点的小球将做周期性运动。则当小球运动的周期最大时,求出磁感应强度B0及运动的最大周期T的大小,并在图中定性画出此时小球运动一个周期的轨迹。